A complex number is a number which can be put in the form a + bi, where a and b are real numbers and i is called the imaginary unit, where i2 = −1. In this expression, a is called the real part and b the imaginary part of the complex number. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the horizontal axis for the real part and the vertical axis for the imaginary part.
The complex number  can be identified with the point (a, b). A complex number whose real part is zero is said to be purely imaginary, whereas a complex number whose imaginary part is zero is a real number. In this way the complex numbers contain the ordinary real numbers while extending them in order to solve problems that cannot be solved with only real numbers.
can be identified with the point (a, b). A complex number whose real part is zero is said to be purely imaginary, whereas a complex number whose imaginary part is zero is a real number. In this way the complex numbers contain the ordinary real numbers while extending them in order to solve problems that cannot be solved with only real numbers.
 can be identified with the point (a, b). A complex number whose real part is zero is said to be purely imaginary, whereas a complex number whose imaginary part is zero is a real number. In this way the complex numbers contain the ordinary real numbers while extending them in order to solve problems that cannot be solved with only real numbers.
can be identified with the point (a, b). A complex number whose real part is zero is said to be purely imaginary, whereas a complex number whose imaginary part is zero is a real number. In this way the complex numbers contain the ordinary real numbers while extending them in order to solve problems that cannot be solved with only real numbers.
Complex numbers are used in many scientific fields, including engineering, electromagnetism, quantum physics, and applied mathematics, such as chaos theory. Italian mathematicianGerolamo Cardano is the first known to have introduced complex numbers. He called them "fictitious", during his attempts to find solutions to cubic equations in the 16th century.
Overview
Complex numbers allow for solutions to certain equations that have no real solution: the equation
has no real solution, since the square of a real number is either 0 or positive. Complex numbers provide a solution to this problem. The idea is to extend the real numbers with the imaginary unit i where 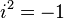 , so that solutions to equations like the preceding one can be found. In this case the solutions are −1 ± 3i. In fact not only quadratic equations, but all polynomial equations in a single variable can be solved using complex numbers.
, so that solutions to equations like the preceding one can be found. In this case the solutions are −1 ± 3i. In fact not only quadratic equations, but all polynomial equations in a single variable can be solved using complex numbers.
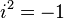 , so that solutions to equations like the preceding one can be found. In this case the solutions are −1 ± 3i. In fact not only quadratic equations, but all polynomial equations in a single variable can be solved using complex numbers.
, so that solutions to equations like the preceding one can be found. In this case the solutions are −1 ± 3i. In fact not only quadratic equations, but all polynomial equations in a single variable can be solved using complex numbers.Definition
A complex number is a number that can be expressed in the form
where a and b are real numbers and i is the imaginary unit, satisfying i2 = −1. For example, −3.5 + 2i is a complex number. It is common to write a for a + 0i and bi for 0 + bi. Moreover, when the imaginary part is negative, it is common to write a − bi with b > 0 instead of a + (−b)i, for example 3 − 4i instead of 3 + (−4)i.
The set of all complex numbers is denoted by  or
or  .
.
 or
or  .
.
The real number a of the complex number z = a + bi is called the real part of z, and the real number b is often called the imaginary part. By this convention the imaginary part is a real number – not including the imaginary unit: hence b, not bi, is the imaginary part.[3][4] The real part is denoted by Re(z) or ℜ(z), and the imaginary part b is denoted by Im(z) or ℑ(z). For example,
Some authors write a+ib instead of a+bi (scalar multiplication between b and i is commutative). In some disciplines, in particular electromagnetism and electrical engineering, j is used instead of i, sincei is frequently used for electric current. In these cases complex numbers are written as a + bj or a + jb.
A real number a can usually be regarded as a complex number with an imaginary part of zero, that is to say, a + 0i. However the sets are defined differently and have slightly different operations defined, for instance comparison operations are not defined for complex numbers. A pure imaginary number is a complex number whose real part is zero, that is to say, of the form 0 + bi.
Complex analysis
Main article: Complex analysis
The study of functions of a complex variable is known as complex analysis and has enormous practical use in applied mathematics as well as in other branches of mathematics. Often, the most natural proofs for statements in real analysis or even number theory employ techniques from complex analysis (see prime number theorem for an example). Unlike real functions which are commonly represented as two-dimensional graphs, complex functions have four-dimensional graphs and may usefully be illustrated by color coding a three-dimensional graph to suggest four dimensions, or by animating the complex function's dynamic transformation of the complex plane.
The notions of convergent series and continuous functions in (real) analysis have natural analogs in complex analysis. A sequence of complex numbers is said to converge if and only if its real and imaginary parts do. This is equivalent to the (ε, δ)-definition of limits, where the absolute value of real numbers is replaced by the one of complex numbers. From a more abstract point of view, C, endowed with the metric
is a complete metric space, which notably includes the triangle inequality
for any two complex numbers z1 and z2.
Like in real analysis, this notion of convergence is used to construct a number of elementary functions: the exponential function exp(z), also written ez, is defined as the infinite series
and the series defining the real trigonometric functions sine and cosine, as well as hyperbolic functions such as sinh also carry over to complex arguments without change. Euler's identity states:
for any real number φ, in particular
Unlike in the situation of real numbers, there is an infinitude of complex solutions z of the equation
for any complex number w ≠ 0. It can be shown that any such solution z—called complex logarithm of a—satisfies
where arg is the argument defined above, and ln the (real) natural logarithm. As arg is a multivalued function, unique only up to a multiple of 2π, log is also multivalued. The principal value of log is often taken by restricting the imaginary part to the interval (−π,π].
Complex exponentiation zω is defined as
Consequently, they are in general multi-valued. For ω = 1 / n, for some natural number n, this recovers the non-unicity of n-th roots mentioned above.
Complex numbers, unlike real numbers, do not in general satisfy the unmodified power and logarithm identities, particularly when naïvely treated as single-valued functions; see failure of power and logarithm identities. For example they do not satisfy
Both sides of the equation are multivalued by the definition of complex exponentiation given here, and the values on the left are a subset of those on the right.
Color wheel graph of sin(1/z). Black parts inside refer to numbers having large absolute values.
See also
- Circular motion using complex numbers
- Complex base systems
- Complex geometry
- Complex square root
- Domain coloring
- Eisenstein integer
- Euler's identity
- Gaussian integer
- Mandelbrot set
- Quaternion
- Riemann sphere (extended complex plane)
- Root of unity





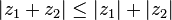










Tidak ada komentar:
Posting Komentar