A series is, informally speaking, the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely.
In mathematics, given an infinite sequence of numbers { an }, a series is informally the result of adding all those terms together: a1 + a2 + a3 + · · ·. These can be written more compactly using the summation symbol ∑. An example is the famous series from Zeno's dichotomy and its mathematical representation:
The terms of the series are often produced according to a certain rule, such as by a formula, or by an algorithm. As there are an infinite number of terms, this notion is often called an infinite series. Unlike finite summations, infinite series need tools from mathematical analysis, and specifically the notion of limits, to be fully understood and manipulated. In addition to their ubiquity in mathematics, infinite series are also widely used in other quantitative disciplines such as physics and computer science.
Definition
For any sequence  of rational numbers, real numbers, complex numbers, functions thereof, etc., the associated series is defined as the ordered formal sum
of rational numbers, real numbers, complex numbers, functions thereof, etc., the associated series is defined as the ordered formal sum
 of rational numbers, real numbers, complex numbers, functions thereof, etc., the associated series is defined as the ordered formal sum
of rational numbers, real numbers, complex numbers, functions thereof, etc., the associated series is defined as the ordered formal sum .
.
The sequence of partial sums  associated to a series
associated to a series  is defined for each
is defined for each 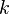 as the sum of the sequence
as the sum of the sequence  from
from  to
to 
 associated to a series
associated to a series  is defined for each
is defined for each 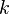 as the sum of the sequence
as the sum of the sequence  from
from  to
to 
 .
.
By definition the series  converges to a limit
converges to a limit 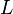 if and only if the associated sequence of partial sums
if and only if the associated sequence of partial sums  converges to
converges to 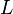 . This definition is usually written as
. This definition is usually written as
 converges to a limit
converges to a limit 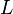 if and only if the associated sequence of partial sums
if and only if the associated sequence of partial sums  converges to
converges to 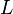 . This definition is usually written as
. This definition is usually written as .
.
More generally, if
 is a function from an index set I to a set G, then the series associated to
is a function from an index set I to a set G, then the series associated to  is the formal sum of the elements
is the formal sum of the elements 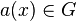 over the index elements
over the index elements 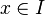 denoted by the
denoted by the .
.
When the index set is the natural numbers
 , the function
, the function  is a sequence denoted by
is a sequence denoted by  . A series indexed on the natural numbers is an ordered formal sum and so we rewrite
. A series indexed on the natural numbers is an ordered formal sum and so we rewrite  as
as  in order to emphasize the ordering induced by the natural numbers. Thus, we obtain the common notation for a series indexed by the natural numbers
in order to emphasize the ordering induced by the natural numbers. Thus, we obtain the common notation for a series indexed by the natural numbers .
.
When the set
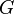 is a semigroup, the sequence of partial sums
is a semigroup, the sequence of partial sums 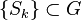 associated to a sequence
associated to a sequence  is defined for each
is defined for each 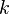 as the sum of the sequence
as the sum of the sequence  from
from  to
to 
 .
.
When the semigroup
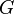 is also a topological space, then the series
is also a topological space, then the series  converges to an element
converges to an element  if and only if the associated sequence of partial sums
if and only if the associated sequence of partial sums  converges to
converges to 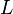 . This definition is usually written as
. This definition is usually written as .
.
Convergent series
A series ∑an is said to 'converge' or to 'be convergent' when the sequence SN of partial sums has a finite limit. If the limit of SN is infinite or does not exist, the series is said to diverge. When the limit of partial sums exists, it is called the sum of the series
An easy way that an infinite series can converge is if all the an are zero for n sufficiently large. Such a series can be identified with a finite sum, so it is only infinite in a trivial sense.
Working out the properties of the series that converge even if infinitely many terms are non-zero is the essence of the study of series. Consider the example
It is possible to "visualize" its convergence on the real number line: we can imagine a line of length 2, with successive segments marked off of lengths 1, ½, ¼, etc. There is always room to mark the next segment, because the amount of line remaining is always the same as the last segment marked: when we have marked off ½, we still have a piece of length ½ unmarked, so we can certainly mark the next ¼. This argument does not prove that the sum is equal to 2 (although it is), but it does prove that it is at most 2. In other words, the series has an upper bound. Proving that the series is equal to 2 requires only elementary algebra, however. If the series is denoted S, it can be seen that
Therefore,
Mathematicians extend the idiom discussed earlier to other, equivalent notions of series. For instance, when we talk about a recurring decimal, as in
we are talking, in fact, just about the series
But since these series always converge to real numbers (because of what is called the completeness property of the real numbers), to talk about the series in this way is the same as to talk about the numbers for which they stand. In particular, it should offend no sensibilities if we make no distinction between 0.111… and 1/9. Less clear is the argument that 9 × 0.111… = 0.999… = 1, but it is not untenable when we consider that we can formalize the proof knowing only that limit laws preserve the arithmetic operations. See 0.999... for more.
Examples
- A geometric series is one where each successive term is produced by multiplying the previous term by a constant number. Example:
-
- In general, the geometric series
- converges if and only if |z| < 1.
- The harmonic series is the series
-
- The harmonic series is divergent.
- An alternating series is a series where terms alternate signs. Example:
- The p-series
-
- converges if r > 1 and diverges for r ≤ 1, which can be shown with the integral criterion described below in convergence tests. As a function of r, the sum of this series is Riemann's zeta function.
-
- converges if the sequence bn converges to a limit L as n goes to infinity. The value of the series is then b1 − L.
Calculus and partial summation as an operation on sequences
Observe that partial summation takes as input a sequence, { an }, and gives as output another sequence, { SN } – partial summation is thus a unary operation on sequences. Further, this function is linear, and thus is a linear operator on the vector space of sequences, denoted Σ. The inverse operator is the finite difference operator, Δ. These behave as discrete analogs of integration and differentiation, only for series (functions of a natural number) instead of functions of a real variable. For example, the sequence {1, 1, 1, ...} has series {1, 2, 3, 4, ...} as its partial summation, which is analogous to the fact that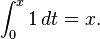 In computer science it is known as prefix sum.Sumber:Wikipedia
In computer science it is known as prefix sum.Sumber:Wikipedia

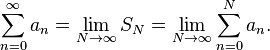







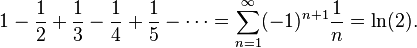




Tidak ada komentar:
Posting Komentar