5.4 Entropy Changes in an Ideal Gas

[VW, S & B: 6.5- 6.6, 7.1]

Many aerospace applications involve flow of gases (e.g., air) and we thus examine the entropy relations for ideal gas behavior. The starting point is form (a) of the combined first and second law,

$\displaystyle du =Tds -Pdv.$

For an ideal gas, . Thus

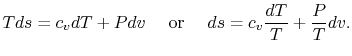
$\displaystyle Tds =c_v dT + Pdv\quad\textrm{ or }\quad ds = c_v \frac{dT}{T}+\frac{P}{T}dv.$

Using the equation of state for an ideal gas ( ), we can write the entropy change as an expression with only exact differentials:

$\displaystyle ds = c_v \frac{dT}{T}+R\frac{dv}{v}.$

(5..2)

We can think of Equation (5.2) as relating the fractional change in temperature to the fractional change of volume, with scale factors and ; if the volume increases without a proportionate decrease in temperature (as in the case of an adiabatic free expansion), then increases. Integrating Equation (5.2) between two states ``1'' and ``2'':

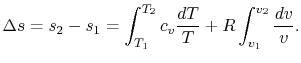
$\displaystyle \Delta s = s_2 - s_1 = \int_{T_1}^{T_2} c_v \frac{dT}{T}+R\int_{v_1}^{v_2}\frac{dv}{v}.$

For a perfect gas with constant specific heats

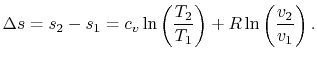
$\displaystyle \Delta s = s_2 - s_1 = c_v \ln\left(\frac{T_2}{T_1}\right)+R\ln\left(\frac{v_2}{v_1}\right).$

In non-dimensional form (using $R/c_v = (\gamma- 1)$ )

$\displaystyle \frac{\Delta s}{c_v}=\ln\left(\frac{T_2}{T_1}\right)+(\gamma-1)\ln\left(\frac{v_2}{v_1}\right),\quad\textrm{ Entropy change of a perfect gas}.$

(5..3)

Equation 5.3 is in terms of specific quantities. For moles of gas,

$\displaystyle \frac{\Delta S}{C_v}=N\left[\ln\left(\frac{T_2}{T_1}\right)+(\gamma-1)\ln\left(\frac{V_2}{V_1}\right)\right].$

This expression gives entropy change in terms of temperature and volume. We can develop an alternative form in terms of pressure and volume, which allows us to examine an assumption we have used. The ideal gas equation of state can be written as

$\displaystyle \ln P + \ln v = \ln R + \ln T.$

Taking differentials of both sides yields

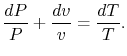
$\displaystyle \frac{dP}{P}+\frac{dv}{v}=\frac{dT}{T}.$

Using the above equation in Eq. (5.2), and making use of the relations

; $c_p/c_v = \gamma$ , we find

$\displaystyle ds = c_v\left[\frac{dP}{P}+\frac{dv}{v}\right] + R\frac{dv}{v},$

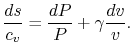
$\displaystyle \frac{ds}{c_v}=\frac{dP}{P}+\gamma\frac{dv}{v}.$

Integrating between two states 1 and 2

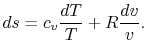
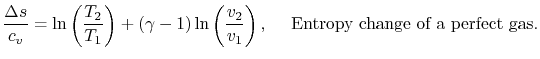
$\displaystyle \frac{\Delta s}{c_v}=\ln\left(\frac{P_2}{P_1}\right)+\gamma\ln\le... ...v_1}\right) =ln\left[\frac{P_2}{P_1}\left(\frac{v_2}{v_1}\right)^\gamma\right].$

(5..4)

Using both sides of (5.4) as exponents we obtain

$\displaystyle \frac{P_2v_2^\gamma}{P_1 v_1^\gamma}=\left[Pv^\gamma\right]^2_1=e^{\Delta s/c_v}.$

(5..5)

Equation (5.5) describes a general process. For the specific situation in which $\Delta s =0$ , i.e., the entropy is constant, we recover the expression $Pv^\gamma = \textrm{constant}$ . It was stated that this expression applied to a reversible, adiabatic process. We now see, through use of the second law, a deeper meaning to the expression, and to the concept of a reversible adiabatic process, in that both are characteristics of a constant entropy, or isentropic, process.