Senin, 02 November 2009

Termodinamika


6.1 Limitations on the Work that Can be Supplied by a Heat Engine

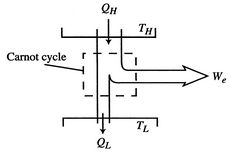
The second law enables us to make powerful and general statements concerning the maximum work that can be derived from any heat engine which operates in a cycle. To illustrate these ideas, we use a Carnot cycle which is shown schematically in Figure 6.1.

Figure 6.1: A Carnot cycle heat engine
Image fig3heatengine_web

The engine operates between two heat reservoirs, exchanging heat $ Q_H$ with the high temperature reservoir at $ T_H$ and $ Q_L$ with the reservoir at $ T_L$ . The entropy changes of the two reservoirs are

>

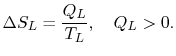0.$">

The same heat exchanges apply to the system, but with opposite signs: the heat received from the high temperature source is positive, and conversely. Denoting the heat transferred to the engines by subscript ``$ e$ '',

$\displaystyle Q_{He} =-Q_H;\quad Q_{Le} =-Q_L.$

The total entropy change during any operation of the engine is

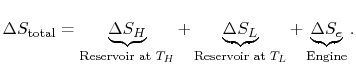
$\displaystyle \Delta S_\textrm{total} = \underbrace{\Delta S_H}_\textrm{Reservo... ...elta S_L}_\textrm{Reservoir at $T_L$} +\underbrace{\Delta S_e}_\textrm{Engine}.$

For a cyclic process, the third of these ( $ \Delta S_e$ )is zero, and thus (remembering that > ),

$\displaystyle \Delta S_\textrm{total} =\Delta S_H +\Delta S_L = \frac{Q_H}{T_H} +\frac{Q_L}{T_L}.$(6..1)

For the engine we can write the first law as

$\displaystyle \Delta U_e =0\; \textrm{(cyclic process)} =Q_{He} +Q_{Le} -W_e.$

Or,

$\displaystyle W_e$$\displaystyle =Q_{He} +Q_{Le}$
$\displaystyle = -Q_H -Q_L.$

Hence, using (6.1)

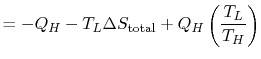$\displaystyle W_e$$\displaystyle =-Q_H -T_L\Delta S_\textrm{total} +Q_H \left(\frac{T_L}{T_H}\right)$
$\displaystyle =-Q_H\left[1-\left(\frac{T_L}{T_H}\right)\right]-T_L\Delta S_\textrm{total}.$

The work of the engine can be expressed in terms of the heat received by the engine as

$\displaystyle W_e=Q_{He}\left[1-\left(\frac{T_L}{T_H}\right)\right]-T_L\Delta S_\textrm{total}.$

The upper limit of work that can be done occurs during a reversible cycle, for which the total entropy change ( $ \Delta S_\textrm{total}$ ) is zero. In this situation:

$\displaystyle \textrm{Maximum work for an engine working between $T_H$ and $T_L$:}\quad W_e =Q_{He}\left[1-\left(\frac{T_L}{T_H}\right)\right].$

Also, for a reversible cycle of the engine,

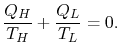
$\displaystyle \frac{Q_H}{T_H} +\frac{Q_L}{T_L} =0.$

These constraints apply to all reversible heat engines operating between fixed temperatures. The thermal efficiency of the engine is

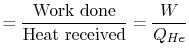$\displaystyle \eta$$\displaystyle = \frac{\textrm{Work done}}{\textrm{Heat received}}=\frac{W}{Q_{He}}$
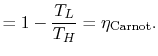$\displaystyle =1-\frac{T_L}{T_H}=\eta_\textrm{Carnot}.$

The Carnot efficiency is thus the maximum efficiency that can occur in an engine working between two given temperatures.

We can approach this last point in another way. The engine work is given by

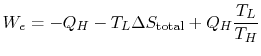
$\displaystyle W_e =-Q_H -T_L\Delta S_\textrm{total} +Q_H \frac{T_L}{T_H}$

or,

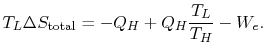
$\displaystyle T_L \Delta S_\textrm{total} =-Q_H +Q_H \frac{T_L}{T_H}-W_e.$

The total entropy change can be written in terms of the Carnot cycle efficiency and the ratio of the work done to the heat absorbed by the engine. The latter is the efficiency of any cycle we can devise:

$\displaystyle \Delta S_\textrm{total} = \frac{Q_{He}}{T_L}\left[1-\frac{T_L}{T_... ...c{Q_{He}}{T_L}\biggl[\eta_\textrm{Carnot}-\eta_\textrm{Any other cycle}\biggr].$

The second law says that the total entropy change is equal to or greater than zero. This means that the Carnot cycle efficiency is equal to or greater than the efficiency for any other cycle, with the total equality only occurring if $ \Delta S_\textrm{total}=0$ .





Muddy Points

So, do we lose the capability to do work when we have an irreversible process and entropy increases? (MP 6.1)

Why do we study cycles starting with the Carnot cycle? Is it because it is easier to work with? (MP 6.2)

Disusun Ulang Oleh:

Arip Nurahman

Pendidikan Fisika, FPMIPA. Universitas Pendidikan Indonesia

&

Follower Open Course Ware at MIT-Harvard University. Cambridge. USA.


Materi kuliah termodinamika ini disusun dari hasil perkuliahan di departemen fisika FPMIPA Universitas Pendidikan Indonesia dengan Dosen:

1. Bpk. Drs. Saeful Karim, M.Si.

2. Bpk. Insan Arif Hidayat, S.Pd., M.Si.

Dan dengan sumber bahan bacaan lebih lanjut dari :

Massachusetts Institute of Technology, Thermodynamics

Professor Z. S. Spakovszk, Ph.D.

Office: 31-265

Phone: 617-253-2196

Email: zolti@mit.edu

Aero-Astro Web: http://mit.edu/aeroastro/people/spakovszky

Gas Turbine Laboratory: home

Ucapan Terima Kasih:

Kepada Para Dosen di MIT dan Dosen Fisika FPMIPA Universitas Pendidikan Indonesia

Semoga Bermanfaat
Diposting oleh di
Label:

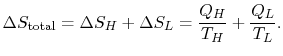
Tidak ada komentar:

Posting Komentar

Langganan: Posting Komentar (Atom)