Disusun Ulang Oleh:
Arip Nurahman
Pendidikan Fisika, FPMIPA. Universitas Pendidikan Indonesia
&
Follower Open Course Ware at MIT-Harvard University. Cambridge. USA.
Materi kuliah termodinamika ini disusun dari hasil perkuliahan di departemen fisika FPMIPA Universitas Pendidikan Indonesia dengan Dosen:
1. Bpk. Drs. Saeful Karim, M.Si.
2. Bpk. Insan Arif Hidayat, S.Pd., M.Si.
Dan dengan sumber bahan bacaan lebih lanjut dari :
Massachusetts Institute of Technology, Thermodynamics
Professor Z. S. Spakovszk, Ph.D.
Office: 31-265
Phone: 617-253-2196
Email: zolti@mit.edu
Aero-Astro Web: http://mit.edu/aeroastro/people/spakovszky
Gas Turbine Laboratory: home
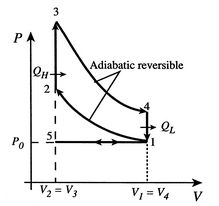
3.5 The Internal combustion engine (Otto Cycle)
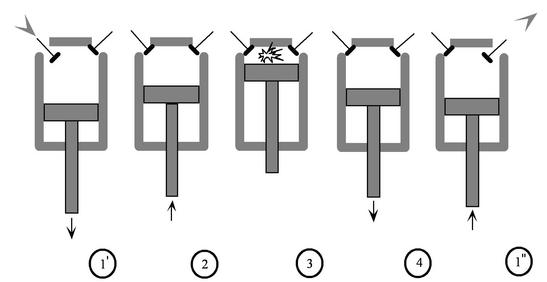
The Otto cycle is a set of processes used by spark ignition internal combustion engines (2-stroke or 4-stroke cycles). These engines a) ingest a mixture of fuel and air, b) compress it, c) cause it to react, thus effectively adding heat through converting chemical energy into thermal energy, d) expand the combustion products, and then e) eject the combustion products and replace them with a new charge of fuel and air. The different processes are shown in Figure 3.8:
- Intake stroke, gasoline vapor and air drawn into engine (
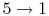 ).
). - Compression stroke,
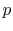 ,
, 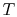 increase (
increase ( 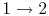 ).
). - Combustion (spark), short time, essentially constant volume (
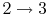 ). Model: heat absorbed from a series of reservoirs at temperatures
). Model: heat absorbed from a series of reservoirs at temperatures 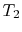 to
to 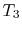 .
. - Power stroke: expansion (
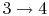 ).
). - Valve exhaust: valve opens, gas escapes.
- (
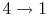 ) Model: rejection of heat to series of reservoirs at temperatures
) Model: rejection of heat to series of reservoirs at temperatures 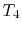 to
to 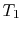 .
. - Exhaust stroke, piston pushes remaining combustion products out of chamber (
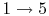 ).
).
We model the processes as all acting on a fixed mass of air contained in a piston-cylinder arrangement, as shown in Figure 3.10.
 |
 |
 |
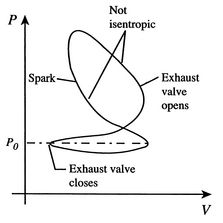
The actual cycle does not have the sharp transitions between the different processes that the ideal cycle has, and might be as sketched in Figure 3.9.
3.5.1 Efficiency of an ideal Otto cycle
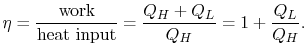
| | ||
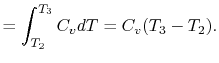 | |
The heat rejected is given by (for a perfect gas with constant specific heats)
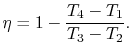
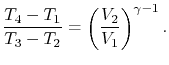
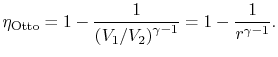
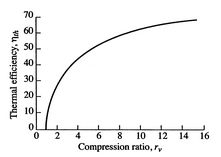 |
The ideal Otto cycle efficiency is shown as a function of the compression ratio in Figure 3.11. As the compression ratio, ![]() , increases,
, increases, ![]() increases, but so does
increases, but so does ![]() . If
. If ![]() is too high, the mixture will ignite without a spark (at the wrong location in the cycle).
is too high, the mixture will ignite without a spark (at the wrong location in the cycle).
3.5.2 Engine work, rate of work per unit enthalpy flux
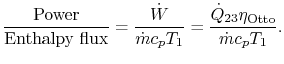
-
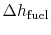 is the heat of reaction, i.e. the chemical energy liberated per unit mass of fuel,
is the heat of reaction, i.e. the chemical energy liberated per unit mass of fuel, -
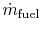 is the fuel mass flow rate.
is the fuel mass flow rate.
![$\displaystyle \frac{\dot{W}}{\dot{m}c_pT_1}=\frac{\dot{m}_\textrm{fuel}}{\dot{m}} \frac{\Delta h_\textrm{fuel}}{c_p T_1}\left[1-\frac{1}{r^{\gamma-1}}\right].$](http://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/img392.png)
| | ||
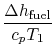 | 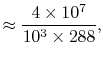 | |
so | ||
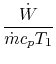 | ![$\displaystyle \approx 9\left[1-\frac{1}{r^{\gamma-1}}\right].$](http://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/img398.png) | |
Muddy Points
How is ![]() calculated? (MP 3.6)
calculated? (MP 3.6)
What are ``stoichiometric conditions?'' (MP 3.7)
Ucapan Terima Kasih:
Kepada Para Dosen di MIT dan Dosen Fisika FPMIPA Universitas Pendidikan Indonesia
Semoga Bermanfaat


Tidak ada komentar:
Posting Komentar