
7.6 Summary and Conclusions
- Entropy as defined from a microscopic point of view is a measure of randomness in a system.
- The entropy is related to the probabilities
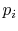 of the individual quantum states of the system bywhere
of the individual quantum states of the system bywhere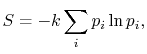
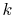 , the Boltzmann constant, is given by
, the Boltzmann constant, is given by 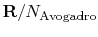 .
. - For a system in which there are
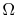 quantum states, all of which are equally probable (for which the probability is
quantum states, all of which are equally probable (for which the probability is 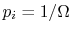 ), the entropy is given by
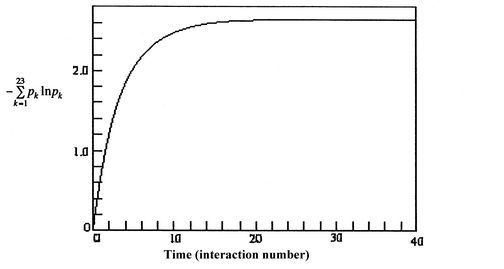
), the entropy is given by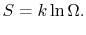 The more quantum states, the more the randomness and uncertainty that a system is in a particular quantum state.
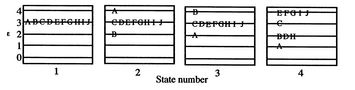
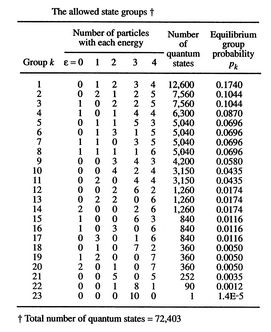
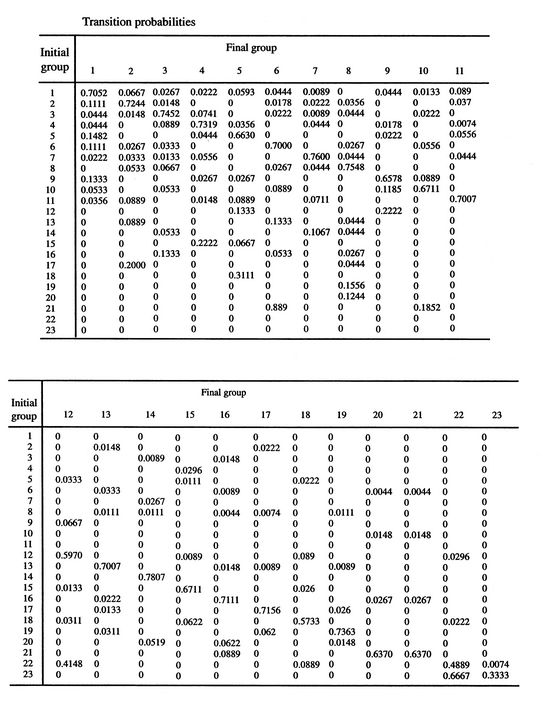
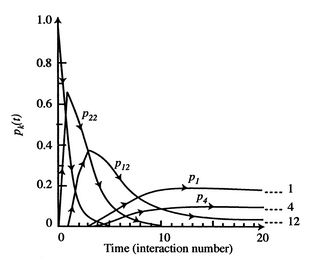
The more quantum states, the more the randomness and uncertainty that a system is in a particular quantum state. - From the statistical point of view there is a finite, but exceedingly small possibility that a system that is well mixed could suddenly ``unmix'' and that all the air molecules in the room could suddenly come to the front half of the room. The unlikelihood of this is well described by Denbigh [Principles of Chemical Equilibrium, 1981] in a discussion of the behavior of an isolated system:
``In the case of systems containing an appreciable number of atoms, it becomes increasingly improbable that we shall ever observe the system in a non-uniform condition. For example, it is calculated that the probability of a relative change of density,
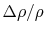 , of only
, of only 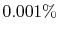 in
in 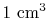 of air is smaller than
of air is smaller than 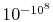 and would not be observed in trillions of years. Thus, according to the statistical interpretation the discovery of an appreciable and spontaneous decrease in the entropy of an isolated system, if it is separated into two parts, is not impossible, but exceedingly improbable. We repeat, however, that it is an absolute impossibility to know when it will take place.''
and would not be observed in trillions of years. Thus, according to the statistical interpretation the discovery of an appreciable and spontaneous decrease in the entropy of an isolated system, if it is separated into two parts, is not impossible, but exceedingly improbable. We repeat, however, that it is an absolute impossibility to know when it will take place.'' - The definition of entropy in the form
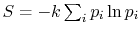 arises in other aerospace fields, notably that of information theory. In this context, the constant
arises in other aerospace fields, notably that of information theory. In this context, the constant 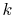 is taken as unity and the entropy becomes a dimensionless measure of the uncertainty represented by a particular message. There is no underlying physical connection with thermodynamic entropy, but the underlying uncertainty concepts are the same.
is taken as unity and the entropy becomes a dimensionless measure of the uncertainty represented by a particular message. There is no underlying physical connection with thermodynamic entropy, but the underlying uncertainty concepts are the same. - The presentation of entropy in this subject is focused on the connection to macroscopic variables and behavior. These involve the definition of entropy given in Chapter 5 of the notes and the physical link with lost work, neither of which makes any mention of molecular (microscopic) behavior. The approach in other sections of the notes is only connected to these macroscopic processes and does not rely at all upon the microscopic viewpoint. Exposure to the statistical definition of entropy, however, is helpful as another way not only to answer the question of ``What is entropy?'' but also to see the depth of this fundamental concept and the connection with other areas of technology.
Disusun Ulang Oleh;
Arip Nurahman
Pendidikan Fisika, FPMIPA. Universitas Pendidikan Indonesia
&
Follower Open Course Ware at MIT-Harvard University, Cambridge. USA.
Semoga Bermanfaat dan Terima Kasih
Materi kuliah termodinamika ini disusun dari hasil perkuliahan di departemen fisika FPMIPA Universitas Pendidikan Indonesia dengan Dosen:
1. Bpk. Drs. Saeful Karim, M.Si.
2. Bpk. Insan Arif Hidayat, S.Pd., M.Si.
Dan dengan sumber bahan bacaan lebih lanjut dari :
Massachusetts Institute of Technology, Thermodynamics
Professor Z. S. Spakovszk, Ph.D.
Office: 31-265
Phone: 617-253-2196
Email: zolti@mit.edu
Aero-Astro Web: http://mit.edu/aeroastro/people/spakovszky
Gas Turbine Laboratory: home
Ucapan Terima Kasih:Kepada Para Dosen di MIT dan Dosen Fisika FPMIPA Universitas Pendidikan Indonesia
Semoga Bermanfaat
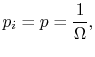
![$\displaystyle = -k \sum_{i=1}^\Omega \frac{1}{\Omega}\ln\left(\frac{1}{\Omega}\... ...ega}\ln\left(\frac{1}{\Omega}\right)\right] =-k\ln\left(\frac{1}{\Omega}\right)$](http://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/img938.png)
![$\displaystyle S=-3k\left[\frac{1}{3}\ln\left(\frac{1}{3}\right)\right]$](http://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/img968.png)

