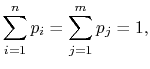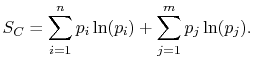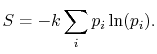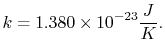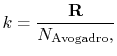7.3 A Statistical Definition of Entropy
There are several attributes that the desired function should have. The first is that the average of the function over all of the microstates should have an extensive behavior. In other words the microscopic description of the entropy of a system ![]() , composed of parts
, composed of parts ![]() and
and ![]() should be given by
should be given by
The average of the function over all the microstates is defined by
where the function
In Equations (7.5) and (7.6), the term ![]() means the probability of a microstate in which system
means the probability of a microstate in which system ![]() is in state
is in state ![]() and system
and system ![]() is in state
is in state ![]() . For Equation (7.4) to hold given the expressions in Equations (7.6),
. For Equation (7.4) to hold given the expressions in Equations (7.6),
The function
To verify this, make this substitution in the expression for ![]() in the first part of Equation (7.6c) (assume the probabilities
in the first part of Equation (7.6c) (assume the probabilities ![]() and
and ![]() are independent, such that
are independent, such that ![]() , and split the log term):
, and split the log term):
Rearranging the sums, (7.8) becomes
Because
the square brackets in the right hand side of Equation (7.9) can be set equal to unity, with the result written as
This reveals the top line of Equation (7.7) to be the same as the bottom line, for any
Based on the above, a statistical definition of entropy can be given as:
The constant
The value of
where
Disusun Ulang Oleh:
Arip Nurahman
Pendidikan Fisika, FPMIPA. Universitas Pendidikan Indonesia
&
Follower Open Course Ware at MIT-Harvard University. Cambridge. USA.
Materi kuliah termodinamika ini disusun dari hasil perkuliahan di departemen fisika FPMIPA Universitas Pendidikan Indonesia dengan Dosen:
1. Bpk. Drs. Saeful Karim, M.Si.
2. Bpk. Insan Arif Hidayat, S.Pd., M.Si.
Dan dengan sumber bahan bacaan lebih lanjut dari :
Massachusetts Institute of Technology, Thermodynamics
Professor Z. S. Spakovszk, Ph.D.
Office: 31-265
Phone: 617-253-2196
Email: zolti@mit.edu
Aero-Astro Web: http://mit.edu/aeroastro/people/spakovszky
Gas Turbine Laboratory: home
Ucapan Terima Kasih:Kepada Para Dosen di MIT dan Dosen Fisika FPMIPA Universitas Pendidikan Indonesia
Semoga Bermanfaat
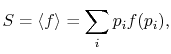
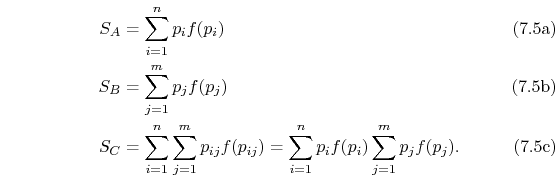
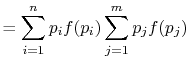
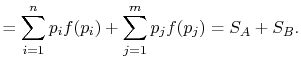
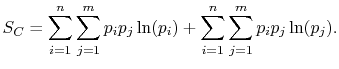
![$\displaystyle S_C = \sum_{i=1}^n\left\{p_i\ln(p_i)\left[\sum_{j=1}^m p_j\right]\right\}+ \sum_{j=1}^m\left\{ p_j\ln(p_j)\left[\sum_{i=1}^n p_i\right]\right\}.$](http://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/img923.png)