Termodinamika

5.2 Axiomatic Statements of the Laws of Thermodynamics

5.2.1 Introduction

As a further aid in familiarization with the second law of thermodynamics and the idea of entropy, we draw an analogy with statements made previously concerning quantities that are closer to experience. In particular, we wish to present once more the Zeroth and First Laws of thermodynamics and use the same framework for the Second Law. In this so-called ``axiomatic formulation,'' the parallels between the Zeroth, First and Second Laws will be made explicit.^5.1

5.2.2 Zeroth Law

Section 1.3.2 presented this observation:

Zeroth Law: There exists for every thermodynamic system in equilibrium a property called temperature. Equality of temperature is a necessary and sufficient condition for thermal equilibrium.

The Zeroth law thus defines a property (temperature) and describes its behavior.

5.2.3 First Law

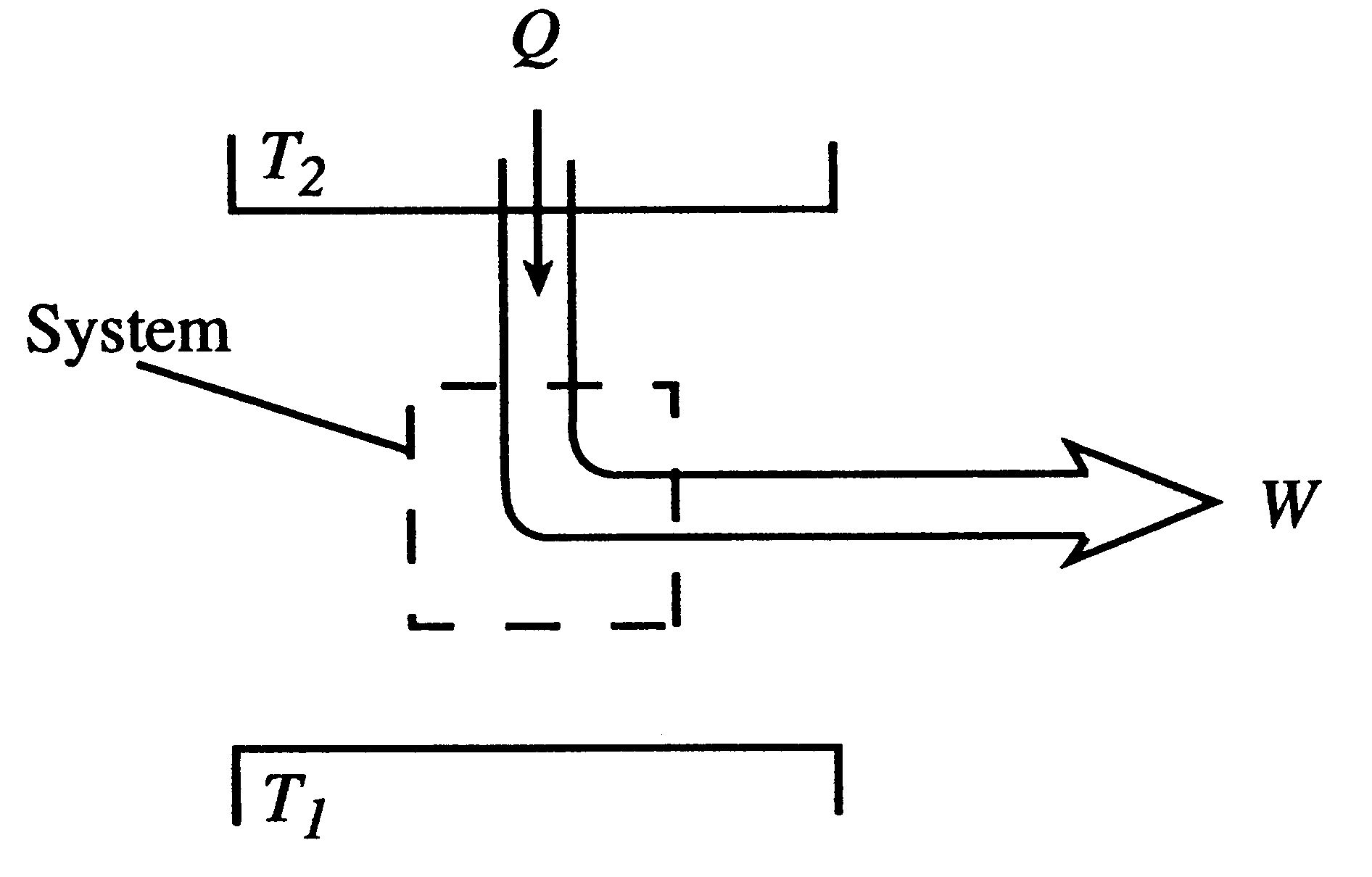
Observations also show that for any system there is a property called the energy. The First Law asserts that one must associate such a property with every system.

First Law: There exists for every thermodynamic system a property called the energy. The change of energy of a system is equal to the mechanical work done on the system in an adiabatic process. In a non-adiabatic process, the change in energy is equal to the heat added to the system minus the mechanical work done by the system.

On the basis of experimental results, therefore, one is led to assert the existence of two new properties, the temperature and internal energy, which do not arise in ordinary mechanics. In a similar way, a further remarkable relationship between heat and temperature will be established, and a new property, the entropy, defined. Although this is a much less familiar property, it is to be stressed that the general approach is quite like that used to establish the Zeroth and First Laws. A general principle and a property associated with any system are extracted from experimental results. Viewed in this way, the entropy should appear no more mystical than the internal energy. The increase of entropy in a naturally occurring process is no less real than the conservation of energy.

5.2.4 Second Law

Although all natural processes must take place in accordance with the First Law, the principle of conservation of energy is, by itself, inadequate for an unambiguous description of the behavior of a system. Specifically, there is no mention of the familiar observation that every natural process has in some sense a preferred direction of action. For example, the flow of heat occurs naturally from hotter to colder bodies, in the absence of other influences, but the reverse flow certainly is not in violation of the First Law. So far as that law is concerned, the initial and final states are symmetrical in a very important respect.

The Second Law is essentially different from the First Law; the two principles are independent and cannot in any sense be deduced from one another. Thus, the concept of energy is not sufficient, and a new property must appear. This property can be developed, and the Second Law introduced, in much the same way as the Zeroth and First Laws were presented. By examination of certain observational results, one attempts to extract from experience a law which is supposed to be general; it is elevated to the position of a fundamental axiom to be proved or disproved by subsequent experiments. Within the structure of classical thermodynamics, there is no proof more fundamental than observations. A statement which can be adopted as the Second Law of thermodynamics is:

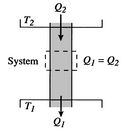
Second Law: There exists for every thermodynamic system in equilibrium an extensive scalar property called the entropy, , such that in an infinitesimal reversible change of state of the system, , where is the absolute temperature and is the amount of heat received by the system. The entropy of a thermally insulated system cannot decrease and is constant if and only if all processes are reversible.

As with the Zeroth and First Laws, the existence of a new property is asserted and its behavior is described.

5.2.5 Reversible Processes

In the course of this development, the idea of a completely reversible process is central, and we can recall the definition, ``a process is called completely reversible if, after the process has occurred, both the system and its surroundings can be wholly restored by any means to their respective initial states'' (first introduced in Section 1.3.3). Especially, it is to be noted that the definition does not, in this form, specify that the reverse path must be identical with the forward path. If the initial states can be restored by any means whatever, the process is by definition completely reversible. If the paths are identical, then one usually calls the process (of the system) reversible, or one may say that the state of the system follows a reversible path. In this path (between two equilibrium states 1 and 2), (i) the system passes through the path followed by the equilibrium states only, and (ii) the system will take the reversed path 2 to 1 by a simple reversal of the work done and heat added.

Reversible processes are idealizations not actually encountered. However, they are clearly useful idealizations. For a process to be completely reversible, it is necessary that it be quasi-static and that there be no dissipative influences such as friction and diffusion. The precise (necessary and sufficient) condition to be satisfied if a process is to be reversible is the second part of the Second Law.

The criterion as to whether a process is completely reversible must be based on the initial and final states. In the form presented above, the Second Law furnishes a relation between the properties defining the two states, and thereby shows whether a natural process connecting the states is possible.

Muddy Points

What happens when all the energy in the universe is uniformly spread, i.e., entropy at a maximum? (MP 5.3)

Disusun Ulang Oleh:

Arip Nurahman

Pendidikan Fisika, FPMIPA. Universitas Pendidikan Indonesia

&

Follower Open Course Ware at MIT-Harvard University. Cambridge. USA.

Materi kuliah termodinamika ini disusun dari hasil perkuliahan di departemen fisika FPMIPA Universitas Pendidikan Indonesia dengan Dosen:

1. Bpk. Drs. Saeful Karim, M.Si.

2. Bpk. Insan Arif Hidayat, S.Pd., M.Si.

Dan dengan sumber bahan bacaan lebih lanjut dari :

Massachusetts Institute of Technology, Thermodynamics

Professor Z. S. Spakovszk, Ph.D.

Office: 31-265

Phone: 617-253-2196

Email: zolti@mit.edu

Aero-Astro Web: http://mit.edu/aeroastro/people/spakovszky

Gas Turbine Laboratory: home

Ucapan Terima Kasih:

Kepada Para Dosen di MIT dan Dosen Fisika FPMIPA Universitas Pendidikan Indonesia

Semoga Bermanfaat

Termodinamika

5.1 Concept and Statements of the Second Law (Why do we need a second law?)

The unrestrained expansion, or the temperature equilibration of the two bricks, are familiar processes. Suppose you are asked whether you have ever seen the reverse of these processes take place? Do two bricks at a medium temperature ever go to a state where one is hot and one is cold? Will the gas in the unrestrained expansion ever spontaneously return to occupying only the left side of the volume? Experience hints that the answer is no. However, both these processes, unfamiliar though they may be, are compatible with the first law. In other words the first law does not prohibit their occurrence. There thus must be some other ``great principle'' that describes the direction of natural processes, that tells us which first law compatible processes will not be observed. This is contained in the second law. Like the first law, it is a generalization from an enormous amount of observation.

There are several ways in which the second law of thermodynamics can be stated. Listed below are three that are often encountered. As described in class (and as derived in almost every thermodynamics textbook), although the three may not appear to have much connection with each other, they are equivalent.

1. No process is possible whose sole result is the absorption of heat from a reservoir and the conversion of this heat into work. [Kelvin-Planck statement of the second law]

   Figure 5.1: This is not possible (Kelvin-Planck)

2. No process is possible whose sole result is the transfer of heat from a cooler to a hotter body. [Clausius statement of the second law]

   Figure 5.2: For
   , this is not possible (Clausius)

3. There exists for every system in equilibrium a property called entropy, , which is a thermodynamic property of a system. For a reversible process, changes in this property are given by
   

   The entropy change of any system and its surroundings, considered together, is positive and approaches zero for any process which approaches reversibility.

   

   For an isolated system, i.e., a system that has no interaction with the surroundings, changes in the system have no effect on the surroundings. In this case, we need to consider the system only, and the first and second laws become:

   
   

   For an isolated system the total energy ( ) is constant. The entropy can only increase or, in the limit of a reversible process, remain constant.

   The limit, or , represents the best that can be done. In thermodynamics, propulsion, and power generation systems we often compare performance to this limit to measure how close to ideal a given process is.

All of these statements are equivalent, but 3 gives a direct, quantitative measure of the departure from reversibility.

Entropy is not a familiar concept and it may be helpful to provide some additional rationale for its appearance. If we look at the first law,

the term on the left is a function of state, while the two terms on the right are not. For a simple compressible substance, however, we can write the work done in a reversible process as , so that

Two out of the three terms in this equation are expressed in terms of state variables. It seems plausible that we ought to be able to express the third term using state variables as well, but what are the appropriate variables? If so, the term should perhaps be viewed as analogous to where the parentheses denote an intensive state variable and the square brackets denote an extensive state variable. The second law tells us that the intensive variable is the temperature, , and the extensive state variable is the entropy, . The first law for a simple compressible substance in terms of state variables is thus

(5..1)

Because Eq. 5.1 includes the second law, it is referred to as the combined first and second law. Because it is written in terms of state variables, it is true for all processes, not just reversible ones.

We summarize below some attributes of entropy:

1. Entropy is a function of the state of the system and can be found if any two properties of the system are known, e.g. or or .
2. is an extensive variable. The entropy per unit mass, or specific entropy, is .
3. The units of entropy are Joules per degree Kelvin (J/K). The units for specific entropy are J/K-kg.
4. For a system, , where the numerator is the heat given to the system and the denominator is the temperature of the system at the location where the heat is received.
5. for pure work transfer.

Muddy Points

Why is always true? (MP 5.1)

What makes different than ? (MP 5.2)

---

Disusun Ulang Oleh:

Arip Nurahman

Pendidikan Fisika, FPMIPA. Universitas Pendidikan Indonesia

&

Follower Open Course Ware at MIT-Harvard University. Cambridge. USA.

Materi kuliah termodinamika ini disusun dari hasil perkuliahan di departemen fisika FPMIPA Universitas Pendidikan Indonesia dengan Dosen:

1. Bpk. Drs. Saeful Karim, M.Si.

2. Bpk. Insan Arif Hidayat, S.Pd., M.Si.

Dan dengan sumber bahan bacaan lebih lanjut dari :

Massachusetts Institute of Technology, Thermodynamics

Professor Z. S. Spakovszk, Ph.D.

Office: 31-265

Phone: 617-253-2196

Email: zolti@mit.edu

Aero-Astro Web: http://mit.edu/aeroastro/people/spakovszky

Gas Turbine Laboratory: home

Ucapan Terima Kasih:

Kepada Para Dosen di MIT dan Dosen Fisika FPMIPA Universitas Pendidikan Indonesia

Semoga Bermanfaat

Termodinamika

4.4 Muddiest Points on Chapter 4

MP 4..1 Why is the ability to do work decreased in B? How do we know?

In state A, the energy is in organized form and the molecules move along circular paths around the spinning flywheel. We could get work out this system by using all of the kinetic energy of the flywheel and for example lift a weight with it. The energy of the system in state B (flywheel not spinning) is associated with disorganized motion (on the molecular scale). The temperature in state B is higher than in state A. We could also extract work from state B by running for example an ideal Carnot cycle between and some heat reservoir at lower temperature. However the work we would get from this ideal Carnot cycle is less than the work we get from state A (all of the kinetic energy), because we must reject some heat when we convert heat into work (we cannot convert heat into 100% work). Although the energy of the system in state A is the same as in state B (we know this from 1^st law) the ``organization'' of the energy is different, and thus the ability to do work is different.

MP 4..2 With the isothermal reversible expansion, is constant? If so, how can we have ?

For a reversible process, if the external pressure were constant, there would need to be a force that pushed on the piston so the process could be considered quasi-equilibrium. This force could be us, it could be a system of weights, or it could be any other work receiver. Under these conditions the system pressure would not necessarily be near the external pressure but we would have . We can of course think of a situation in which the external pressure was varied so it was always close to the system pressure, but that is not necessary.

MP 4..3 Why is the work done equal to zero in the free expansion?

In this problem, the system is everything inside the rigid container. There is no change in volume, no `` ,'' so no work done on the surroundings. Pieces of the gas might be expanding, pushing on other parts of the gas, and doing work locally inside the container (and other pieces might be compressed and thus receive work) during the free expansion process, but we are considering the system as a whole, and there is no net work done.

MP 4..4 Is irreversibility defined by whether or not a mark is left on the outside environment?

A process is irreversible when there is no way to undo the change without leaving a mark on the surroundings or ``the rest of the universe.'' In the example with the bricks, we could undo the change by putting a Carnot refrigerator between the bricks (both at after putting them together) and cooling one brick down to and heating the other brick to to restore the initial state. To do this we have to supply work to the refrigerator and we will also reject some heat to the surroundings. Thus we leave a mark on the environment and the process is irreversible.

MP 4..5 Is heat transfer across a finite temperature difference only irreversible if no device is present between the two to harvest the potential difference?

If we have two heat reservoirs at different temperatures, the irreversibility associated with the transfer of heat from one to the other is indeed dependent on what is between them. If there is a copper bar between them, all the heat that comes out of the high temperature reservoir goes into the low temperature reservoir, with the result given in Section 5.5. If there were a Carnot cycle between them, some (not all) heat from the high temperature reservoir would be passed on to the low temperature reservoir, the process would be reversible, and work would be done. The extent to which the process is irreversible for any device can be assessed by computing the total entropy change (device plus surroundings) associated with the heat transfer.

Disusun Ulang Oleh:

Arip Nurahman

Pendidikan Fisika, FPMIPA. Universitas Pendidikan Indonesia

&

Follower Open Course Ware at MIT-Harvard University. Cambridge. USA.

Materi kuliah termodinamika ini disusun dari hasil perkuliahan di departemen fisika FPMIPA Universitas Pendidikan Indonesia dengan Dosen:

1. Bpk. Drs. Saeful Karim, M.Si.

2. Bpk. Insan Arif Hidayat, S.Pd., M.Si.

Dan dengan sumber bahan bacaan lebih lanjut dari :

Massachusetts Institute of Technology, Thermodynamics

Professor Z. S. Spakovszk, Ph.D.

Office: 31-265

Phone: 617-253-2196

Email: zolti@mit.edu

Aero-Astro Web: http://mit.edu/aeroastro/people/spakovszky

Gas Turbine Laboratory: home

Ucapan Terima Kasih:

Kepada Para Dosen di MIT dan Dosen Fisika FPMIPA Universitas Pendidikan Indonesia

Semoga Bermanfaat

Termodinamika

4.3 Features of reversible processes

[VW, S & B: 6.3-6.4]

Reversible processes are idealizations or models of real processes. One familiar and widely used example is Bernoulli's equation, which you saw in Unified. They are extremely useful for defining limits to system or device behavior, for enabling identification of areas in which inefficiencies occur, and in giving targets for design.

An important feature of a reversible process is that, depending on the process, it represents the maximum work that can be extracted in going from one state to another, or the minimum work that is needed to create the state change.

Let us consider processes that do work, so that we can show that the reversible one produces the maximum work of all possible processes between two states. For example, suppose we have a thermally insulated cylinder that holds an ideal gas, Figure 4.9. The gas is contained by a thermally insulated massless piston with a stack of many small weights on top of it. Initially the system is in mechanical and thermal equilibrium.

Figure 4.9:A piston with weights on top

Consider the following three processes, shown in Figure 4.10:

1. All of the weights are removed from the piston instantaneously and the gas expands until its volume is increased by a factor of four (a free expansion).
2. Half of the weight is removed from the piston instantaneously, the system is allowed to double in volume, and then the remaining half of the weight is instantaneously removed from the piston and the gas is allowed to expand until its volume is again doubled.
3. Each small weight is removed from the piston one at a time, so that the pressure inside the cylinder is always in equilibrium with the weight on top of the piston. When the last weight is removed, the volume has increased by a factor of four.

   Figure 4.10: Getting the most work out of a system requires that the work be extracted reversibly

   Maximum work (proportional to the area under these curves) is obtained for the quasi-static expansion.

To reiterate:

• The work done by a system during a reversible process is the maximum work we can get.
• The work done on a system in a reversible process is the minimum work we need to do to achieve that state change.

A process must be quasi-static (quasi-equilibrium) to be reversible. This means that the following effects must be absent or negligible:

1. Friction: If we would have to do net work to bring the system from one volume to another and return it to the initial condition (recall Section 1.3.3.)
2. Free (unrestrained) expansion.
3. Heat transfer through a finite temperature difference.

Figure 4.11: Heat transfer across a finite temperature difference

Suppose we have heat transfer from a high temperature to a lower temperature as shown in Figure 4.11. How do we restore the situation to the initial conditions? One thought would be to run a Carnot refrigerator to get an amount of heat, , from the lower temperature reservoir to the higher temperature reservoir. We could do this but the surroundings, again us, would need to provide some amount of work (which we could find using our analysis of the Carnot refrigerator). The net (and only) result at the end of the combined process would be a conversion of an amount of work into heat. For reversible heat transfer from a heat reservoir to a system, the temperatures of the system and the reservoir must be . In other words the difference between the temperatures of the two entities involved in the heat transfer process can only differ by an infinitesimal amount, .

While all natural processes are irreversible to some extent, it cannot be emphasized too strongly that there are a number of engineering situations where the effect of irreversibility can be neglected and the reversible process furnishes an excellent approximation to reality.

The second law, which is the next topic we address, allows us to make a quantitative statement concerning the irreversibility of a given physical process.

Figure 4.12:Nicolas Sadi Carnot (1796-1832), an engineer and an officer in the French army. Carnot's work is all the more remarkable because it was made without the benefit of either the first or second law. The second law was not discovered until 30 years later. [Atkins, The Second Law]

Muddy Points

Is heat transfer across a finite temperature difference only irreversible if no device is present between the two to harvest the potential difference? (MP 4.5)

Disusun Ulang Oleh:

Arip Nurahman

Pendidikan Fisika, FPMIPA. Universitas Pendidikan Indonesia

&

Follower Open Course Ware at MIT-Harvard University. Cambridge. USA.

Materi kuliah termodinamika ini disusun dari hasil perkuliahan di departemen fisika FPMIPA Universitas Pendidikan Indonesia dengan Dosen:

1. Bpk. Drs. Saeful Karim, M.Si.

2. Bpk. Insan Arif Hidayat, S.Pd., M.Si.

Dan dengan sumber bahan bacaan lebih lanjut dari :

Massachusetts Institute of Technology, Thermodynamics

Professor Z. S. Spakovszk, Ph.D.

Office: 31-265

Phone: 617-253-2196

Email: zolti@mit.edu

Aero-Astro Web: http://mit.edu/aeroastro/people/spakovszky

Gas Turbine Laboratory: home

Ucapan Terima Kasih:

Kepada Para Dosen di MIT dan Dosen Fisika FPMIPA Universitas Pendidikan Indonesia

Semoga Bermanfaat