
Universitas Pendidikan Indonesia.
Pertemuan
10-18
Ujian
Pertemuan ke-11; 17-11-2009
1. Mentafakuri dan Memaknai Film 2012
Pertemuan ke-10; 10-11-2009
Sumber: Drs. Saeful Karim, M.Si.
a. Kekuatan Hidup
b. Kekuatan Spiritual
“Film ini bukan ramalan, karena sang sutradara tidak memastikan hal tersebut pasti terjadi, namun ini adalah sebuah peringatan, bahwa bumi ini sudah tua.”
“Bumi ini perlu dibarukan, dengan system yang baru, dengan kehidupan yang baru. Apa yang terjadi akhir-akhir ini adalah upaya alam untuk menuju keseimbangan”
Ruh dari Hukum-hukum Termodinamika
1. Kekekalan Energi, Kuantitatif, dianalogikan seperti kita menerima uang Rp. 500.000,- dari orang tua dan kita mendistribusikan uang itu keberbagai sektor untuk memenuhi kebutuhan, cukup sampai disana, tidak ada pertanyaan: Dipakai apa? Dan Apa pentingnya?
2. Mengenai Entropi, Kulaitatif, ini sudah menyangkut kualitatif dimana semua aspek perlu dipertanyakan mengenai (efisiensinya/Nilai Manfaat):
Analoginya
a. Uang yang diberikan dari orang tua kita itu, dipakai untuk apa? Seberapa pentingnya? Apa manfaatnya? Berhubungan dengan Kehidupan atau Akademik kita? Dan seterusnya.
Q-------àW
Tugas manusia adalah menggunakan Q untuk seefisien-efiseinnya menghasilkan W
Tapi mesti diingat bahwasannya; “Sehebat-hebatnya efisiensi tidak mungkin mencapai 1, Efisiensi =/ 1
“Efisiensi itu harus ditinjau dari segala aspek, boleh kita meningkatkan efisiensi setinggi-tingginya namun jangan menabrak hukum alam”
“Setiap orang bisa mencari uang, namun tidak semua orang mampu menggunakannya dengan efisien”
Pojok Al-Quran:1. Q.S. Al-Zatsiah; 45:16
2. Q.S. Al-Baqoroh; 62
3. Q.S. Al-Isro; 72
4. Q.S. Al-Kahfi 103-106
Iman Kepada Tuhan:
1. Memanajemen Hati (MQ)
2. Jadikan diri Kita Bermanfaat bagi orang lain.
Bani Israel = “Orang-orang yang berjalan menuju Tuhan”
Analogi Mengejar Akhirat dan Dunia
Matahari Manusia Bayangan
Pertemuan Ke-12: 24-11-2009:
Siklus Carnot dan Reversibilitas : Proses reversibilitas dan irreversibel, siklus Carnot, prinsip-prinsip Carnot, skala temperatur termodinamika, mesin kalor Carnot, mesin pendingin dan pompa panas Carnot, siklus Otto-Siklus ideal untuk mesin berbahan bakar bensin, dan siklus Diesel- siklus ideal untuk mesin berbahan bakar solar.
Pertemuan Ke-13: 01-12-2009:
Gas Ideal : Persamaan keadaan gas (nyata dan ideal), faktor kompresibilitas, energi dalam gas (nyata dan ideal), konsep gas ideal, persamaan-persamaan keadaan berbagai sistem termodinamika, penentuan kapasitas panas eksperimental, dan proses adiabatik quasistatik.
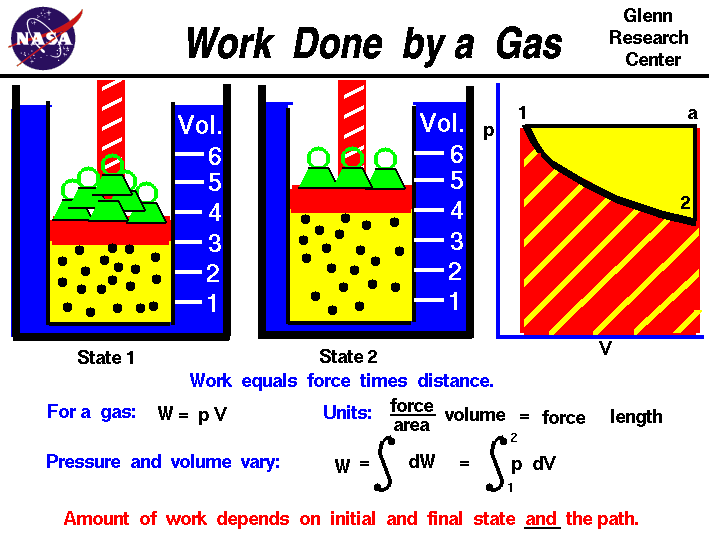
Thermodynamics is a branch of physics which deals with the energy and work of a system. Thermodynamics deals only with the large scale response of a system which we can observe and measure in experiments. In aerodynamics, we are most interested in the thermodynamics of high speed flows, and in propulsion systems which produce thrust by accelerating a gas. To understand how thrust is created, it is useful to study the basic thermodynamics of gases.
The state of a gas is determined by the values of certain measurable properties like the pressure, temperature, and volume which the gas occupies. The values of these variables and the state of the gas can be changed. On this figure we show a gas confined in a blue jar in two different states. On the left, in State 1, the gas is at a higher pressure and occupies a smaller volume than in State 2, at the right. We can represent the state of the gas on a graph of pressure versus volume, which is called a p-V diagram as shown at the right. To change the state of the gas from State 1 to State 2, we must change the conditions in the jar, either by heating the gas, or physically changing the volume by moving a piston, or by changing the pressure by adding or removing weights from the piston. In some of these changes, we do work on, or have work done by the gas, in other changes we add, or remove heat. Thermodynamics helps us determine the amount of work and the amount of heat necessary to change the state of the gas. Notice that in this example we have a fixed mass of gas. We can therefore plot either the physical volume or the specific volume, volume divided by mass, since the change is the same for a constant mass. On the figure, we use physical volume.
Scientists define work W to be the product of force F acting through a distance s :
W = F * s
For a gas, work is the product of the pressure p and the volume V during a change of volume.
W = p * V
We can do a quick units check to see that pressure force / area times volume area * length gives units of force times length which are the units of work
W = (force / area) * (area * length) = force * length
In the metric system the unit of work is the Joule, in the English system the unit is the foot-pound. In general, during a change of state both the volume and the pressure change. So it is more correct to define the work as the integrated, or summed variable pressure times the change of volume from State 1 to State 2. If we use the symbol S [ ] ds for integral, then:
W = S [p] dV
On a graph of pressure versus volume, the work is the area under the curve that describes how the state is changed from State 1 to State 2.
As mentioned above, there are several options for changing the state of a gas from one state to another. So we might expect that the amount of work done on, or by a gas could be different depending on exactly how the state is changed. As an example, on the graph on the figure, we show a curved black line from State 1 to State 2 of our confined gas. This line represents a change brought about by removing weights and decreasing the pressure and allowing the volume to adjust according to Boyle's law with no heat addition. The line is curved and the amount of work done on the gas is shown by the red shaded area below this curve. We could, however, move from State 1 to State 2 by holding the pressure constant and increasing the volume by heating the gas using Charles' law. The resulting change in state proceeds from State 1 to an intermediate State "a" on the graph. State "a" is at the same pressure as State 1, but at a different volume. If we then remove the weights, holding a constant volume, we proceed on to State 2. The work done in this process is shown by the yellow shaded area. Using either process we change the state of the gas from State 1 to State 2. But the work for the constant pressure process is greater than the work for the curved line process. The work done by a gas not only depends on the initial and final states of the gas but also on the process used to change the state. Different processes can produce the same state, but produce different amounts of work.
Notice that not only does the work done by the gas depend on the process, but also the heat transferred to the gas. In the first process, the curved line from State 1 to State2, no heat was transferred to the gas; the process was adiabatic. But in the second process, the straight line from State 1 to State "a" and then to State 2, heat was transferred to the gas during the constant pressure process. The heat transferred to a gas not only depends on the initial and final states of the gas but also on the process used to change the state.
Pertemuan Ke-14: 08-12-2009:
Entropi I : Persamaan dan pertidaksamaan Clausius, entropi, prinsip perubahan entropi, perubahan entropi pada berbagai proses, apa itu entropi ?, digram entropi, hubungan TdS, perubahan entropi zat murni, perubahan entropi zat padat dan zat cair.

Thermodynamics is a branch of physics which deals with the energy and work of a system. Thermodynamics deals only with the large scale response of a system which we can observe and measure in experiments. In aerodynamics, we are most interested in thermodynamics in the study of propulsion systems and understanding high speed flows.
The state of a gas is defined by several properties including the temperature, pressure, and volume which the gas occupies. From a study of the first law of thermodynamics, we find that the internal energy of a gas is also a state variable, that is, a variable which depends only on the state of the gas and not on any process that produced that state. We are free to define additional state variables which are combinations of existing state variables. The new variables often make the analysis of a system much simpler. For a gas, a useful additional state variable is the enthalpy which is defined to be the sum of the internal energy E plus the product of the pressure p and volume V. Using the symbol H for the enthalpy:
H = E + p * V
The enthalpy can be made into an intensive, or specific , variable by dividing by the mass. Propulsion engineers use the specific enthalpy in engine analysis more than the enthalpy itself.
How does one use this new variable called enthalpy? Let's consider the first law of thermodynamics for a gas. For a system with heat transfer Q and work W, the change in internal energy E from state 1 to state 2 is equal to the difference in the heat transfer into the system and the work done by the system:
E2 - E1 = Q - W
The work and heat transfer depend on the process used to change the state. For the special case of a constant pressure process, the work done by the gas is given as the constant pressure p times the change in volume V:
W = p * [V2 - V1]
Substituting into the first equation, we have:
E2 - E1 = Q - p * [V2 - V1]
Let's group the conditions at state 2 and the conditions at state 1 together:
(E2 + p * V2) - (E1 + p * V1) = Q
The (E + p * V) can be replaced by the enthalpy H.
H2 - H1 = Q
From our definition of the heat transfer, we can represent Q by some heat capacity coefficient Cp times the temperature T.
(H2 - H1) = Cp * (T2 - T1)
At the bottom of the slide, we have divided by the mass of gas to produce the specific enthalpy equation version.
(h2 - h1) = cp * (T2 - T1)
The specific heat capacity cp is called the specific heat at constant pressure and is related to the universal gas constant of the equation of state. This final equation is used to determine values of specific enthalpy for a given temperature. Enthalpy is used in the energy equation for a fluid. Across shock waves, the total enthalpy of the gas remains a constant.
Pertemuan Ke-15: 15-12-2009:
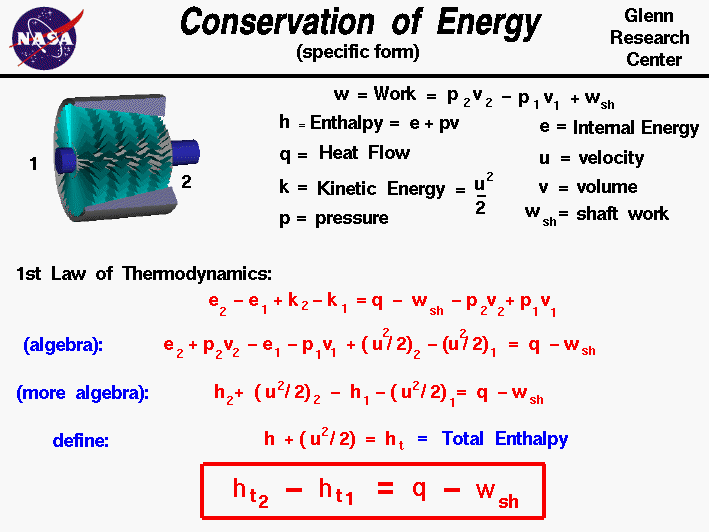
The conservation of energy is a fundamental concept of physics along with the conservation of mass and the conservation of momentum. Within some problem domain, the amount of energy remains constant and energy is neither created nor destroyed. Energy can be converted from one form to another (potential energy can be converted to kinetic energy) but the total energy within the domain remains fixed.
Thermodynamics is a branch of physics which deals with the energy and work of a system. As mentioned on the gas properties slide, thermodynamics deals only with the large scale response of a system which we can observe and measure in experiments. In rocketry, we are most interested in thermodynamics in the study of propulsion systems and understanding high speed flows.
On some separate slides, we have discussed the state of a static gas, the properties which define the state, and the first law of thermodynamics as applied to any system, in general. On this slide we derive a useful form of the energy conservation equation for a gas beginning with the first law of thermodynamics. If we call the internal energy of a gas E, the work done by the gas W, and the heat transferred into the gas Q, then the first law of thermodynamics indicates that between state "1" and state "2":
E2 - E1 = Q - W
Aerospace engineers usually simplify a thermodynamic analysis by using intensive variables; variables that do not depend on the mass of the gas. We call these variables specific variables. We create a "specific" variable by taking a property whose value depends on the mass of the system and dividing it by the mass of the system. Many of the state properties listed on this slide, such as the work and internal energy depend on the total mass of gas. We will use "specific" versions of these variables. Engineers usually use the lower case letter for the "specific" version of a variable. Our first law equation then becomes:
e2 - e1 = q - w
Because we are considering a moving gas, we add the specific kinetic energy term to the internal energy on the left side. The normal kinetic energy K of a moving substance is equal to 1/2 times the mass m times the velocity u squared:
K = (m * u^2) / 2
Then the specific kinetic energy k is given by:
k = (u^2) / 2
and the first law equation becomes:
e2 - e1 + k2 - k1 = q - w
There are two parts to the specific work for a moving gas. Some of the work, called the shaft work (wsh) is used to move the fluid or turn a shaft, while the rest of the work goes into changing the state of the gas. For a pressure p and specific volume v, the work is given by:
w = (p * v)2 - (p * v)1 + wsh
Substituting:
e2 - e1 + k2 - k1 = q - (p * v)2 + (p * v)1 - wsh
If we perform a little algebra on the first law of thermodynamics, we can begin to group some terms of the equations. :
e2 + (p * v)2 - e1 - (p * v)1 + [(u^2) / 2]2 - [(u^2) / 2]1 = q - wsh
A useful additional state variable for a gas is the specific enthalpy h which is equal to:
h = e + (p * v)
Simplifying the energy equation:
h2 - h1 + [(u^2) / 2]2 - [(u^2) / 2]1 = q - wsh
orh2 + [(u^2) / 2]2 - h1 - [(u^2) / 2]1 = q - wsh
By combining the velocity terms with the enthalpy terms to form the total specific enthalpy "ht" we can further simplify the equation.
ht = h + u^2 / 2
The total specific enthalpy is analogous to the total pressure in Bernoulli's equation; both expressions involve a "static" value plus one half the square of the velocity.
The final, most useful, form of the energy equation is given in the red box.
ht2 - ht1 = q - wsh
For a compressor or power turbine, there is no external heat flow into the gas and the "q" term is set equal to zero. In the burner, no work is performed and the "wsh" term is set to zero.
Entropi II :
Pertemuan Ke-16: 22-12-2009
Perumusan Lengkap Termodinamika : Persamaan-persamaan Maxwell, hubungan umum untuk dU, dS, dH, dG, dF, Cv, dan Cp, DH, DS, DU berbagai gas.
Pertemuan Ke-17: 29-12-2009

Thermodynamics is a branch of physics which deals with the energy and work of a system. Thermodynamics deals only with the large scale response of a system which we can observe and measure in experiments. In aerodynamics, the thermodynamics of a gas obviously plays an important role in the analysis of propulsion systems but also in the understanding of high speed flows. The first law of thermodynamics defines the relationship between the various forms of energy present in a system (kinetic and potential), the work which the system performs and the transfer of heat. The first law states that energy is conserved in all thermodynamic processes.
We can imagine thermodynamic processes which conserve energy but which never occur in nature. For example, if we bring a hot object into contact with a cold object, we observe that the hot object cools down and the cold object heats up until an equilibrium is reached. The transfer of heat goes from the hot object to the cold object. We can imagine a system, however, in which the heat is instead transferred from the cold object to the hot object, and such a system does not violate the first law of thermodynamics. The cold object gets colder and the hot object gets hotter, but energy is conserved. Obviously we don't encounter such a system in nature and to explain this and similar observations, thermodynamicists proposed a second law of thermodynamics. Clasius, Kelvin, and Carnot proposed various forms of the second law to describe the particular physics problem that each was studying. The description of the second law stated on this slide was taken from Halliday and Resnick's textbook, "Physics". It begins with the definition of a new state variable called entropy. Entropy has a variety of physical interpretations, including the statistical disorder of the system, but for our purposes, let us consider entropy to be just another property of the system, like enthalpy or temperature.
The second law states that there exists a useful state variable called entropy S. The change in entropy delta S is equal to the heat transfer delta Q divided by the temperature T.
delta S = delta Q / T
For a given physical process, the combined entropy of the system and the environment remains a constant if the process can be reversed. If we denote the initial and final states of the system by "i" and "f":
Sf = Si (reversible process)
An example of a reversible process is ideally forcing a flow through a constricted pipe. Ideal means no boundary layer losses. As the flow moves through the constriction, the pressure, temperature and velocity change, but these variables return to their original values downstream of the constriction. The state of the gas returns to its original conditions and the change of entropy of the system is zero. Engineers call such a process an isentropic process. Isentropic means constant entropy.
The second law states that if the physical process is irreversible, the combined entropy of the system and the environment must increase. The final entropy must be greater than the initial entropy for an irreversible process:
Sf > Si (irreversible process)
An example of an irreversible process is the problem discussed in the second paragraph. A hot object is put in contact with a cold object. Eventually, they both achieve the same equilibrium temperature. If we then separate the objects they remain at the equilibrium temperature and do not naturally return to their original temperatures. The process of bringing them to the same temperature is irreversible.
Pertemuan Ke-18: 05-01-2010
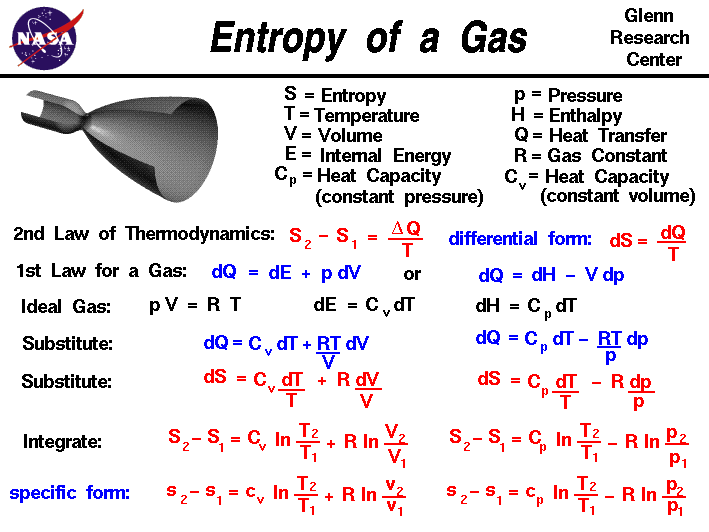
Thermodynamics is a branch of physics that deals with the energy and work of a system. In aerodynamics, we are most interested in thermodynamics in the study of propulsion systems and understanding high speed flows. The first law of thermodynamics indicates that the total energy of a system is conserved. Total energy includes the potential and kinetic energy, the work done by the system, and the transfer of heat through the system. The second law of thermodynamics indicates that, while many physical processes that satisfy the first law are possible, the only processes that occur in nature are those for which the entropy of the system either remains constant or increases.
Entropy, like temperature and pressure, can be explained on both a macro scale and a micro scale. Since thermodynamics deals only with the macro scale, the change in entropy delta S is defined here to be the heat transfer delta Q into the system divided by the temperature T:
delta S = delta Q / T
During a thermodynamic process, the temperature T of an object changes as heat Q is applied or extracted. A more correct definition of the entropy S is the differential form that accounts for this variation.
dS = dQ / T
The change in entropy is then the inverse of the temperature integrated over the change in heat transfer. For gases, there are two possible ways to evaluate the change in entropy. We begin by using the first law of thermodynamics:
dE = dQ - dW
where E is the internal energy and W is the work done by the system. Substituting for the definition of work for a gas.
dQ = dE + p dV
where p is the pressure and V is the volume of the gas. If we use the definition of the enthalpy H of a gas:
H = E + p * V
Then:
dH = dE + p dV + V dp
Substitute into the first law equation:
dQ = dH - V dp - p dV + p dV
dQ = dH - V dp
is an alternate way to present the first law of thermodynamics. For an ideal gas, the equation of state is written:
p * V = R * T
where R is the gas constant. The heat transfer of a gas is equal to the heat capacity times the change in temperature; in differential form:
dQ = C * dT
If we have a constant volume process, the formulation of the first law gives:
dE = dQ = C (constant volume) * dT
dH = dQ = C (constant pressure) * dT
dQ = C (constant volume) * dT + R * T dV / V
Similarly substituting the value of V from the equation of state, and the definition of dH we obtain the alternate form:
dQ = C (constant pressure) * dT - R * T dp / p
Substituting these forms for dQ into the differential form of the entropy equation gives::
dS = C (constant volume) * dT / T + R * dV / V
and
dS = C (constant pressure) * dT / T - R * dp / p
These equations can be integrated from condition "1" to condition "2" to give:
S2 - S1 = Cv * ln ( T2 / T1) + R * ln ( V2 / V1)
and
S2 - S1 = Cp * ln ( T2 / T1) - R * ln ( p2 / p1)
where Cv is the heat capacity at constant volume, Cp is the heat capacity at constant pressure, and ln is the symbol for the logarithmic function.
If we divide both equations by the mass of gas, we can obtain intrinsic, or "specific" forms of both equations:s2 - s1 = cv * ln ( T2 / T1) + R * ln ( v2 / v1)
and
s2 - s1 = cp * ln ( T2 / T1) - R * ln ( p2 / p1)
where cp and cv are the specific heat capacities. Depending on the type of process we encounter, we can now determine the change in entropy for a gas.
These equations can be a bit confusing, because we use the specific heat at constant volume when we have a process that changes volume, and the specific heat at constant pressure when the process changes pressure.To clarify matters, let's look at the first equation:
s2 - s1 = cv * ln ( T2 / T1) + R * ln ( v2 / v1)
If we have a constant volume process, the second term in the equation is equal to zero, since v2/v1 = 1. We can then determine the value of the specific heat for the constant volume process. But if we have a process that changes volume, the second term in the equation is not zero. We can think of the first term of the equation as the contribution for a constant volume process, and the second term as the additional change produced by the change in volume. A similar type of argument can be made for the equation used for a change in pressure.
Disusun Ulang Oleh:
Arip Nurahman
Pendidikan Fisika, FPMIPA. Universitas Pendidikan Indonesia
&
Follower Open Course Ware at MIT-Harvard University, Cambridge. USA.
Sumber:
1. Perkuliahan Termodinamika Fisika UPI
2. Nasa Glenn Research Center
Ucapan Terima kasih:
1. Bapak Saeful Karim
2. Insan Arif H
Catatan: Laman Ini Selalu di perbaharui apa bila ada kesalahan, mohon masukannya




Tidak ada komentar:
Posting Komentar