Pertemuan Ke-1; Selasa, 08-09-2009
Pendahuluan Termodinamika
“Saya mengajarkan akhlak dan hidup dalam Termodinamika, dan salah satu kebahagiaan utama guru adalah siswanya lebih hebat dan berhasil dari gurunya”
~Saeful Karim~
Bagian: 1, Sekilas
Termodinamika (bahasa Yunani: thermos = 'panas' and dynamic = 'perubahan'):
adalah fisika energi , panas, kerja, entropi dan kespontanan proses. Termodinamika berhubungan dekat dengan mekanika statistik di mana banyak hubungan termodinamika berasal. Pada sistem di mana terjadi proses perubahan wujud atau pertukaran energi, termodinamika klasik tidak berhubungan dengan kinetika reaksi (kecepatan suatu proses reaksi berlangsung). Karena alasan ini, penggunaan istilah "termodinamika" biasanya merujuk pada termodinamika setimbang. Dengan hubungan ini, konsep utama dalam termodinamika adalah proses kuasistatik, yang diidealkan, proses "super pelan". Proses termodinamika bergantung-waktu dipelajari dalam termodinamika tak-setimbang.
Karena termodinamika tidak berhubungan dengan konsep waktu, telah diusulkan bahwa termodinamika setimbang seharusnya dinamakan termostatik.
Hukum termodinamika kebenarannya sangat umum, dan hukum-hukum ini tidak bergantung kepada rincian dari interaksi atau sistem yang diteliti. Ini berarti mereka dapat diterapkan ke sistem di mana seseorang tidak tahu apa pun kecual perimbangan transfer energi dan wujud di antara mereka dan lingkungan. Contohnya termasuk perkiraan Einstein tentang emisi spontan dalam abad ke-20 dan riset sekarang ini tentang termodinamika benda hitam.
Juga mempelajari dan mengkaji transformasi energinya.
Hukum-hukum Dasar Termodinamika
Terdapat empat Hukum Dasar yang berlaku di dalam sistem termodinamika, yaitu:
The laws of thermodynamics describe the transport of heat and work in thermodynamic processes. These laws have become some of the most important in all of physics and other types of science associated with thermodynamics.
Classical thermodynamics, which is focused on systems in thermodynamic equilibrium, can be considered separately from non-equilibrium thermodynamics. This article focuses on classical or thermodynamic equilibrium thermodynamics.
The four principles (referred to as "laws"):
- 1. The zeroth law of thermodynamics, which underlies the definition of temperature.
- 2. The first law of thermodynamics, which mandates conservation of energy, and states in particular that the flow of heat is a form of energy transfer.
- 3. The second law of thermodynamics, which states that the entropy of an isolated macroscopic system never decreases, or (equivalently) thatperpetual motion machines are impossible.
- 4. The third law of thermodynamics, which concerns the entropy of a perfect crystal at absolute zero temperature, and implies that it is impossible to cool a system all the way to exactly absolute zero.
During the last 80 years writers have suggested additional laws, but none of them have become well accepted.
Hukum Awal (Zeroth Law) Termodinamika
Hukum ini menyatakan bahwa dua sistem dalam keadaan setimbang dengan sistem ketiga, maka ketiganya dalam saling setimbang satu dengan lainnya.
Main article: Zeroth law of thermodynamics
If two thermodynamic systems are each in thermal equilibrium with a third, then they are in thermal equilibrium with each other.
When two systems are put in contact with each other, there will be a net exchange of energy between them unless or until they are in thermal equilibrium. That is the state of having equal temperature. Although this concept of thermodynamics is fundamental, the need to state it explicitly was not widely perceived until the first third of the 20th century, long after the first three principles were already widely in use. Hence it was numbered zero -- before the subsequent three. The Zeroth Law asserts that thermal equilibrium, viewed as a binary relation, is atransitive relation (and since any system is always in equilibrium with itself and if a system is in equilibrium with another, the latter is in equilibrium with the former, it is furthermore anequivalence relation).
Hukum Pertama Termodinamika
Hukum ini terkait dengan kekekalan energi. Hukum ini menyatakan perubahan energi dalam dari suatu sistem termodinamika tertutup sama dengan total dari jumlah energi kalor yang disuplai ke dalam sistem dan kerja yang dilakukan terhadap sistem.
Energy can neither be created nor destroyed. It can only change forms.
In any process in an isolated system, the total energy remains the same.
The First Law states that energy cannot be created or destroyed; rather, the amount of energy lost in a steady state process cannot be greater than the amount of energy gained. This is the statement of conservation of energy for a thermodynamic system. It refers to the two ways that a closed system transfers energy to and from its surroundings – by the process of heating (or cooling) and the process of mechanical work. The rate of gain or loss in the stored energy of a system is determined by the rates of these two processes. In open systems, the flow of matter is another energy transfer mechanism, and extra terms must be included in the expression of the first law.
The First Law clarifies the nature of energy. It is a stored quantity which is independent of any particular process path, i.e., it is independent of the system history. If a system undergoes athermodynamic cycle, whether it becomes warmer, cooler, larger, or smaller, then it will have the same amount of energy each time it returns to a particular state. Mathematically speaking, energy is a state function and infinitesimal changes in the energy are exact differentials.
All laws of thermodynamics but the First are statistical and simply describe the tendencies of macroscopic systems. For microscopic systems with few particles, the variations in the parameters become larger than the parameters themselves, and the assumptions of thermodynamics become meaningless.
Fundamental thermodynamic relation
The first law can be expressed as the fundamental thermodynamic relation:
Heat supplied to a system = increase in internal energy of the system + work done by the system
Increase in internal energy of a system = heat supplied to the system - work done by the system

Here, E is internal energy, T is temperature, S is entropy, p is pressure, and V is volume. This is a statement of conservation of energy: The net change in internal energy (dE) equals the heat energy that flows in (TdS), minus the energy that flows out via the system performing work (pdV).
Hukum kedua Termodinamika
Hukum kedua termodinamika terkait dengan entropi. Hukum ini menyatakan bahwa total entropi dari suatu sistem termodinamika terisolasi cenderung untuk meningkat seiring dengan meningkatnya waktu, mendekati nilai maksimumnya.
The entropy of an isolated system consisting of two regions of space, isolated from one another, each in thermodynamic equilibrium in itself, but not in equilibrium with each other, will, when the isolation that separates the two regions is broken, so that the two regions become able to exchange matter or energy, tend to increase over time, approaching a maximum value when the jointly communicating system reaches thermodynamic equilibrium.
In a simple manner, the second law states "energy systems have a tendency to increase their entropy rather than decrease it." This can also be stated as "heat can spontaneously flow from a higher-temperature region to a lower-temperature region, but not the other way around." Heat can appear to flow from cold to hot, for example, when a warm object is cooled in a refrigerator, but the transfer of energy is still from hot to cold. The heat from the object warms the surrounding air, which in turn heats and expands the refrigerant. The refrigerant is then compressed, expending electrical energy.
A way of thinking about the second law for non-scientists is to consider entropy as a measure of ignorance of the microscopic details of the system. So, for example, one has less knowledge about the separate fragments of a broken cup than about an intact one, because when the fragments are separated, one does not know exactly whether they will fit together again, or whether perhaps there is a missing shard. Solid crystals, the most regularly structured form of matter, have very low entropy values; and gases, which are very disorganized, have high entropy values. This is because the positions of the crystal atoms are more predictable than are those of the gas atoms.
The entropy of an isolated macroscopic system never decreases. However, a microscopic system may exhibit fluctuations of entropy opposite to that stated by the Second Law (seeMaxwell's demon and Fluctuation Theorem).
Hukum ketiga Termodinamika
Hukum ketiga termodinamika terkait dengan temperatur nol absolut. Hukum ini menyatakan bahwa pada saat suatu sistem mencapai temperatur nol absolut, semua proses akan berhenti dan entropi sistem akan mendekati nilai minimum. Hukum ini juga menyatakan bahwa entropi benda berstruktur kristal sempurna pada temperatur nol absolut bernilai nol.
Briefly, this postulates that entropy is temperature dependent and results in the formulation of the idea of absolute zero.
Tentative fourth laws or principles
Over the years, various thermodynamic researchers have come forward to ascribe to or to postulate potential fourth laws of thermodynamics (either suggesting that a widely-accepted principle should be called the fourth law, or proposing entirely new laws); in some cases, even fifth or sixth laws of thermodynamics are proposed[2]. Most fourth law statements, however, are speculative and controversial.
The most commonly proposed Fourth Law is the Onsager reciprocal relations, which give a quantitative relation between the parameters of a system in which heat and matter are simultaneously flowing.
Other tentative fourth law statements are attempts to apply thermodynamics to evolution. During the late 19th century, thermodynamicist Ludwig Boltzmann argued that the fundamental object of contention in the life-struggle in the evolution of the organic world is 'available energy'. Another example is the maximum power principle as put forward initially by biologist Alfred Lotka in his 1922 article Contributions to the Energetics of Evolution.[3] Most variations of hypothetical fourth laws (or principles) have to do with the environmental sciences, biological evolution, or galactic phenomena.[4]
History
The first established principle which eventually became the Second Law was formulated by Sadi Carnot during 1824. By 1860, as formalized in the works of those such as Rudolf Clausiusand William Thomson, there were two established "principles" of thermodynamics, the first principle and the second principle. As the years passed, these principles were termed "laws." By 1873, for example, thermodynamicist Josiah Willard Gibbs, in his “Graphical Methods in the Thermodynamics of Fluids”, clearly stated that there were two absolute laws of thermodynamics, a first law and a second law.
Pertemuan Ke-2; Selasa, 15-09-2009
“Jangan takut miskin karena jujur”
~Saeful Karim~
Bagian 1:
Konsep-Konsep Dasar Termodinamika
Pengabstrakan dasar atas termodinamika adalah pembagian dunia menjadi sistem dibatasi oleh kenyataan atau ideal dari batasan. Sistem yang tidak termasuk dalam pertimbangan digolongkan sebagai lingkungan. Dan pembagian sistem menjadi subsistem masih mungkin terjadi, atau membentuk beberapa sistem menjadi sistem yang lebih besar. Biasanya sistem dapat diberikan keadaan yang dirinci dengan jelas yang dapat diuraikan menjadi beberapa parameter.
Sistem Termodinamika
Sistem termodinamika adalah bagian dari jagat raya yang diperhitungkan. Sebuah batasan yang nyata atau imajinasi memisahkan sistem dengan jagat raya, yang disebut lingkungan. Klasifikasi sistem termodinamika berdasarkan pada sifat batas sistem-lingkungan dan perpindahan materi, kalor dan entropi antara sistem dan lingkungan.
Ada tiga jenis sistem berdasarkan jenis pertukaran yang terjadi antara sistem dan lingkungan:
§ sistem terisolasi: tak terjadi pertukaran panas, benda atau kerja dengan lingkungan. Contoh dari sistem terisolasi adalah wadah terisolasi, seperti tabung gas terisolasi.
§ sistem tertutup: terjadi pertukaran energi (panas dan kerja) tetapi tidak terjadi pertukaran benda dengan lingkungan. Rumah hijau adalah contoh dari sistem tertutup di mana terjadi pertukaran panas tetapi tidak terjadi pertukaran kerja dengan lingkungan. Apakah suatu sistem terjadi pertukaran panas, kerja atau keduanya biasanya dipertimbangkan sebagai sifat pembatasnya:
§ pembatas adiabatik: tidak memperbolehkan pertukaran panas.
§ pembatas rigid: tidak memperbolehkan pertukaran kerja.
§ sistem terbuka: terjadi pertukaran energi (panas dan kerja) dan benda dengan lingkungannya. Sebuah pembatas memperbolehkan pertukaran benda disebut permeabel. Samudra merupakan contoh dari sistem terbuka.
Dalam kenyataan, sebuah sistem tidak dapat terisolasi sepenuhnya dari lingkungan, karena pasti ada terjadi sedikit pencampuran, meskipun hanya penerimaan sedikit penarikan gravitasi. Dalam analisis sistem terisolasi, energi yang masuk ke sistem sama dengan energi yang keluar dari sistem.
KEADAAN TERMODINAMIKA
Ketika sistem dalam keadaan seimbang dalam kondisi yang ditentukan, ini disebut dalam keadaan pasti (atau keadaan sistem).Untuk keadaan termodinamika tertentu, banyak sifat dari sistem dispesifikasikan. Properti yang tidak tergantung dengan jalur di mana sistem itu membentuk keadaan tersebut, disebut fungsi keadaan dari sistem. Bagian selanjutnya dalam seksi ini hanya mempertimbangkan properti, yang merupakan fungsi keadaan.
Jumlah properti minimal yang harus dispesifikasikan untuk menjelaskan keadaan dari sistem tertentu ditentukan oleh Hukum fase Gibbs. Biasanya seseorang berhadapan dengan properti sistem yang lebih besar, dari jumlah minimal tersebut.Pengembangan hubungan antara properti dari keadaan yang berlainan dimungkinkan. Persamaan keadaan adalah contoh dari hubungan tersebut.
Thermodynamic process
A thermodynamic process may be defined as the energetic evolution of a thermodynamic system proceeding from an initial state to a final state. Typically, each thermodynamic process is distinguished from other processes, in energetic character, according to what parameters, as temperature, pressure, or volume, etc., are held fixed. Furthermore, it is useful to group these processes into pairs, in which each variable held constant is one member of a conjugate pair. The seven most common thermodynamic processes are shown below:
1. An isobaric process occurs at constant pressure.
2. An isochoric process, or isometric/isovolumetric process, occurs at constant volume.
3. An isothermal process occurs at a constant temperature.
4. An adiabatic process occurs without loss or gain of energy by heat.
5. An isentropic process (reversible adiabatic process) occurs at a constant entropy.
6. An isenthalpic process occurs at a constant enthalpy.
7. A steady state process occurs without a change in the internal energy of a system.
A thermodynamic potential is a scalar potential function used to represent the thermodynamic state of a system. One main thermodynamic potential which has a physical interpretation is the internal energy, U. It is the energy of configuration of a given system of conservative forces (that is why it is a potential) and only has meaning with respect to a defined set of references (or data). Expressions for all other thermodynamic energy potentials are derivable via Legendre transforms from an expression for U. Inthermodynamics, certain forces, such as gravity, are typically disregarded when formulating expressions for potentials. For example, while all the working fluid in a steam engine may have higher energy due to gravity while sitting on top of Mt. Everest than it would at the bottom of the Mariana trench, the gravitational potential energy term in the formula for the internal energy would usually be ignored because changes in gravitational potential within the engine during operation would be negligible. Five common thermodynamic energy potentials are:
where T = temperature, S = entropy, p = pressure, V = volume. The Helmholtz free energy is often denoted by the symbol F, but the use of A is preferred by IUPAC [2]. Ni is the number of particles of type i in the system and μi is the chemical potential for an i-type particle. For the sake of completeness, the set of all Ni are also included as natural variables, although they are sometimes ignored. These five common potentials are all energy potentials, but there are also entropy potentials.
Pertemuan Ke-3; Selasa, 22-09-2009
1. Arti Limit dan Kesadaran,
"Limit (mendekati nol) itu tidak pernah menghasilkan nol, sekecil apapun pasti akan ada nilainya.
Kebaikan sekecil apapun, sekalipun niat, itu ada nilanya.
sekalipun gagal tetap akan ada nilainya dan bukan nol.
Hidup nol jika tidak ada nilai
Kita tidak ada nilai jika kita tidak ada karya
Karya tidak akan ada jika kita tidak ...ada usaha
sedangkan usaha akan nol jika tidak ada perpindahan (Pola pikir, Jasad/kerja)
Jika nilai kita nol, apa bedanya dengan yang ada di alam kubur?
Selama Tuhan masih memberikan waktu kepada kita untuk hidup."
Kita masih ada HARAPAN
~Power Ranger, B. Ach~
Selamat Berkarya
Matematika Termodinamika I
1. Dasar-dasar Matematika Termodinamika
2. Diferensial Fungsi Variabel Tunggal
3. Diferensial Fungsi Dua Variabel
4. Pengertian Fungsi Diferensiabel
| Other conventional variables |
| W | Work done by the system on its surroundings |
| Q | Heat transferred from the surroundings into the system |
Sifat-sifat Zat Murni : Zat murni, fase-fase zat murni, proses perubahan fase zat murni, diagram proses perubahan fase zat murni, diagram permukaan P-V-T.
Pertemuan Ke-4; 29-09-2009
“Kemuliaanmu tergantung seberapa cerdas menggunakan ilmu yang kau miliki”
~Pascal~
1. Keprofesionalan Guru (Pendidikan Profesi Guru)
http://pk.sps.upi.edu/index.html
(Pus Bang Kurikulum UPI)
Dalam manajemen sumber daya manusia, menjadi profesional adalah tuntutan jabatan, pekerjaan ataupun profesi. Ada satu hal penting yang menjadi aspek bagi sebuah profesi, yaitu sikap profesional dan kualitas kerja. Profesional (dari bahasa Inggris) berarti ahli, pakar, mumpuni dalam bidang yang digeluti.
Menjadi profesional, berarti menjadi ahli dalam bidangnya. Dan seorang ahli, tentunya berkualitas dalam melaksanakan pekerjaannya. Akan tetapi tidak semua Ahli dapat menjadi berkualitas. Karena menjadi berkualitas bukan hanya persoalan ahli, tetapi juga menyangkut persoalan integritas dan personaliti. Dalam perspektif pengembangan sumber daya manusia, menjadi profesional adalah satu kesatuan antara konsep personaliti dan integritas yang dipadupadankan dengan skil atau keahliannya.
Menjadi profesional adalah tuntutan setiap profesi, seperti dokter, insinyur, pilot, ataupun profesi yang telah familiar ditengah masyarakat. Akan tetapi guru...? Sudahkan menjadi profesi dengan kriteria diatas. Guru jelas sebuah profesi. Akan tetapi sudahkah ada sebuah profesi yang profesional...? Minimal menjadi guru harus memiliki keahlian tertentu dan distandarkan secara kode keprofesian. Apabila keahlian tersebut tidak dimiliki, maka tidak dapat disebut guru. Artinya tidak sembarangan orang bisa menjadi guru.
Suhu dan Hukum kenol termodinamika : Kesetimbangan termal, konsep temperatur, pengukuran temperatur, besaran termometric, jenis-jenis termometer berdasarkan besaran termometricnya, temperatur gas ideal, penskalaan termometer, dan termokopel.
2. Matematika Termodinamika II
a. Diferensial Eksak dan Tak Eksak
b. Hubungan Penting antara Diferensial Parsial
c. Penerapan Diferensial Parsial Pada Sistem Termodinamika
3. Koordinat Termodinamika, (Makro; Terasa dan terlihat,seperti tekanan volume dan lain-lain Mikro, yang tidak terindra, seperti kecepatan partikel energy dalam, massa tiap partikel, tinjauan per satuan masa)
For one dimension, a differential

is always exact.
For two dimensions, in order that a differential

be an exact differential in a simply-connected region R of the xy-plane, it is necessary and sufficient that between A and B there exists the relation:

For three dimensions, a differential

is an exact differential in a simply-connected region R of the xyz-coordinate system if between the functions A, B and C there exist the relations:
 ;
;  ;
; 
These conditions are equivalent to the following one: If G is the graph of this vector valued function then for all tangent vectors X,Y of the surface G then s(X,Y)=0 with s the symplectic form.
These conditions, which are easy to generalize, arise from the independence of the order of differentiations in the calculation of the second derivatives. So, in order for a differential dQ, that is a function of four variables to be an exact differential, there are six conditions to satisfy.
In summary, when a differential dQ is exact:
- the function Q exists;
 , independent of the path followed.
, independent of the path followed.
In thermodynamics, when dQ is exact, the function Q is a state function of the system. The thermodynamic functions U, S, H, A and G are state functions. Generally, neither work nor heatis a state function. An exact differential is sometimes also called a 'total differential', or a 'full differential', or, in the study of differential geometry, it is termed an exact form.
Partial differential relations
For three variables, x, y and z bound by some differentiable function F(x,y,z), the following total differentials exist[1]:667&669

 .
.- Note: The subscripts outside the parenthesis indicate which variables are being held constant during differentiation. Due to the definition of the partial derivative, these subscripts are not required, but they are included as a reminder.
Substituting the first equation into the second and rearranging, we obtain[1]:669
![d z = {\left ( \frac{\partial z}{\partial x} \right )}_y \left [ {\left ( \frac{\partial x}{\partial y} \right )}_z d y + {\left ( \frac{\partial x}{\partial z} \right )}_y dz \right ] + {\left ( \frac{\partial z}{\partial y} \right )}_x dy](http://upload.wikimedia.org/math/5/2/c/52c67ba0dc0e3e7fdfc6879c5ed0170e.png) ,
,![d z = \left [ {\left ( \frac{\partial z}{\partial x} \right )}_y {\left ( \frac{\partial x}{\partial y} \right )}_z + {\left ( \frac{\partial z}{\partial y} \right )}_x \right ] d y + {\left ( \frac{\partial z}{\partial x} \right )}_y {\left ( \frac{\partial x}{\partial z} \right )}_y dz](http://upload.wikimedia.org/math/4/3/3/4336933c06624ec3f8b22470046eec2b.png) ,
,![\left [ 1 - {\left ( \frac{\partial z}{\partial x} \right )}_y {\left ( \frac{\partial x}{\partial z} \right )}_y \right ] dz = \left [ {\left ( \frac{\partial z}{\partial x} \right )}_y {\left ( \frac{\partial x}{\partial y} \right )}_z + {\left ( \frac{\partial z}{\partial y} \right )}_x \right ] d y](http://upload.wikimedia.org/math/e/3/9/e39cc3e51cf0a0a942d2b23be1e61ea2.png) .
.
Since y and z are independent variables, dy and dz may be chosen without restriction. For this last equation to hold in general, the bracketed terms must be equal to zero.[1]:669
Reciprocity relation
Setting the first term in brackets equal to zero yields[1]:670
 .
.
A slight rearrangement gives a reciprocity relation,[1]:670
 .
.
There are two more permutations of the foregoing derivation that give a total of three reciprocity relations between x, y and z. Reciprocity relations show that the inverse of a partial derivative is equal to its reciprocal.
Cyclic relation
Setting the second term in brackets equal to zero yields[1]:670
 .
.
Using a reciprocity relation for  on this equation and reordering gives a cyclic relation (the triple product rule),[1]:670
on this equation and reordering gives a cyclic relation (the triple product rule),[1]:670
 .
.
If, instead, a reciprocity relation for 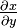 is used with subsequent rearrangement, a standard form for implicit differentiation is obtained:
is used with subsequent rearrangement, a standard form for implicit differentiation is obtained:
 .
.
Some useful equations derived from exact differentials in two dimensions
(See also Bridgman's thermodynamic equations for the use of exact differentials in the theory of thermodynamic equations)
Suppose we have five state functions z,x,y,u, and v. Suppose that the state space is two dimensional and any of the five quantites are exact differentials. Then by the chain rule

but also by the chain rule:

and
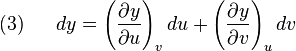
so that:
![(4)~~~~~ dz = \left[ \left(\frac{\partial z}{\partial x}\right)_y \left(\frac{\partial x}{\partial u}\right)_v + \left(\frac{\partial z}{\partial y}\right)_x \left(\frac{\partial y}{\partial u}\right)_v \right]du](http://upload.wikimedia.org/math/e/b/4/eb4403091698adde7d61fa6caed95c8c.png)
![+ \left[ \left(\frac{\partial z}{\partial x}\right)_y \left(\frac{\partial x}{\partial v}\right)_u + \left(\frac{\partial z}{\partial y}\right)_x \left(\frac{\partial y}{\partial v}\right)_u \right]dv](http://upload.wikimedia.org/math/0/5/0/0502fc18d6b162fda0d70f94a537a388.png)
which implies that:

Letting v = y gives:

Letting u = y gives:

Letting u = y, v = z gives:

using ( gives the triple product rule:
gives the triple product rule:

Oleh:





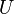
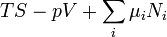



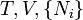
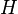

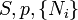



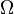









 , independent of the path followed.
, independent of the path followed.
 .
.![d z = {\left ( \frac{\partial z}{\partial x} \right )}_y \left [ {\left ( \frac{\partial x}{\partial y} \right )}_z d y + {\left ( \frac{\partial x}{\partial z} \right )}_y dz \right ] + {\left ( \frac{\partial z}{\partial y} \right )}_x dy](http://upload.wikimedia.org/math/5/2/c/52c67ba0dc0e3e7fdfc6879c5ed0170e.png) ,
,![d z = \left [ {\left ( \frac{\partial z}{\partial x} \right )}_y {\left ( \frac{\partial x}{\partial y} \right )}_z + {\left ( \frac{\partial z}{\partial y} \right )}_x \right ] d y + {\left ( \frac{\partial z}{\partial x} \right )}_y {\left ( \frac{\partial x}{\partial z} \right )}_y dz](http://upload.wikimedia.org/math/4/3/3/4336933c06624ec3f8b22470046eec2b.png) ,
,![\left [ 1 - {\left ( \frac{\partial z}{\partial x} \right )}_y {\left ( \frac{\partial x}{\partial z} \right )}_y \right ] dz = \left [ {\left ( \frac{\partial z}{\partial x} \right )}_y {\left ( \frac{\partial x}{\partial y} \right )}_z + {\left ( \frac{\partial z}{\partial y} \right )}_x \right ] d y](http://upload.wikimedia.org/math/e/3/9/e39cc3e51cf0a0a942d2b23be1e61ea2.png) .
. .
. .
. .
. on this equation and reordering gives a cyclic relation (the
on this equation and reordering gives a cyclic relation (the  .
.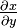 is used with subsequent rearrangement, a
is used with subsequent rearrangement, a  .
.

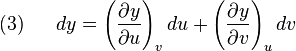
![(4)~~~~~ dz = \left[ \left(\frac{\partial z}{\partial x}\right)_y \left(\frac{\partial x}{\partial u}\right)_v + \left(\frac{\partial z}{\partial y}\right)_x \left(\frac{\partial y}{\partial u}\right)_v \right]du](http://upload.wikimedia.org/math/e/b/4/eb4403091698adde7d61fa6caed95c8c.png)
![+ \left[ \left(\frac{\partial z}{\partial x}\right)_y \left(\frac{\partial x}{\partial v}\right)_u + \left(\frac{\partial z}{\partial y}\right)_x \left(\frac{\partial y}{\partial v}\right)_u \right]dv](http://upload.wikimedia.org/math/0/5/0/0502fc18d6b162fda0d70f94a537a388.png)




 gives the
gives the 

