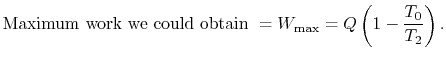Photo by: Something Surprising

6.6 Entropy and Unavailable Energy (Lost Work by Another Name)

Consider a system consisting of a heat reservoir at in surroundings (the atmosphere) at . The surroundings are equivalent to a second reservoir at . For an amount of heat, , transferred from the reservoir, the maximum work we could derive is times the thermal efficiency of a Carnot cycle operated between these two temperatures:

$\displaystyle \textrm{Maximum work we could obtain } = W_\textrm{max} =Q\left(1 -\frac{T_0}{T_2}\right).$

(6..7)

Only part of the heat transferred can be turned into work, in other words only part of the heat energy is available to be used as work.

Suppose we transferred the same amount of heat from the reservoir directly to another reservoir at a temperature . The maximum work available from the quantity of heat, , before the transfer to the reservoir at is

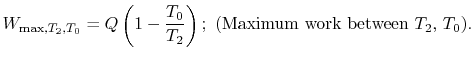
$\displaystyle W_\textrm{max,$T_2$,$T_0$} =Q\left(1 -\frac{T_0}{T_2}\right); \textrm{ (Maximum work between $T_2$, $T_0$)}.$

The maximum amount of work available after the transfer to the reservoir at

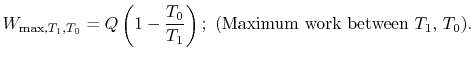
$\displaystyle W_\textrm{max,$T_1$,$T_0$} =Q\left(1 -\frac{T_0}{T_1}\right); \textrm{ (Maximum work between $T_1$, $T_0$)}.$

There is an amount of energy that could have been converted to work prior to the irreversible heat transfer process of magnitude

$\displaystyle E'$	$\displaystyle = Q\left[\left(1-\frac{T_0}{T_2}\right)-\left(1-\frac{T_0}{T_1}\right)\right] =Q\left[\frac{T_0}{T_1}-\frac{T_0}{T_2}\right],$
or
$\displaystyle E'$	$\displaystyle = T_0\left[\frac{Q}{T_1}-\frac{Q}{T_2}\right].$

However,

is the entropy gain of the reservoir at

and (

) is the entropy decrease of the reservoir at

. The amount of energy,

, that could have been converted to work (but now cannot be) can therefore be written in terms of entropy changes and the temperature of the surroundings as

$\displaystyle E'$	$\displaystyle =T_0\left(\Delta S_\textrm{reservoir at $T_1$}+\Delta S_\textrm{reservoir at $T_2$}\right)$
	$\displaystyle =T_0 \Delta S_\textrm{irreversible heat transfer process}$
$\displaystyle E'$	$\displaystyle =\textrm{\lq\lq Lost work,'' or energy which is no longer available to do work.}$

The situation just described is a special case of an important principle concerning entropy changes, irreversibility and the loss of capability to do work. We thus now develop it in a more general fashion, considering an arbitrary system undergoing an irreversible state change, which transfers heat to the surroundings (for example the atmosphere), which can be assumed to be at constant temperature, . The change in internal energy of the system during the state change is $\Delta U = Q -W$ . The change in entropy of the surroundings is (with the heat transfer to the system)

$\displaystyle \Delta S_\textrm{surroundings} = -\frac{Q}{T_0}.$

Now consider restoring the system to the initial state by a reversible process. To do this we need to do work, $W_\textrm{rev}$ , on the system and extract from the system a quantity of heat, $Q_\textrm{rev}$ . (We did this, for example, in ``undoing'' the free expansion process.) The change in internal energy is (with the quantities $Q_\textrm{rev}$ and $W_\textrm{rev}$ both regarded, in this example, as positive for work done by the surroundings and heat given to the surroundings)^6.2.

$\displaystyle \Delta U_\textrm{rev} =-Q_\textrm{rev} +W_\textrm{rev}.$

In this reversible process, the entropy of the surroundings is changed by

$\displaystyle \Delta S_\textrm{surroundings} =\frac{Q_\textrm{rev}}{T}.$

For the combined changes (the irreversible state change and the reversible state change back to the initial state), the energy change is zero because the energy is a function of state,

$\displaystyle \Delta U_\textrm{rev} +\Delta U =0 =Q -W + (-Q_\textrm{rev} +W_\textrm{rev}).$

Thus,

$\displaystyle Q_\textrm{rev} -Q =W_\textrm{rev} -W.$

For the system, the overall entropy change for the combined process is zero, because the entropy is a function of state,

$\displaystyle \Delta S_\textrm{system, combined process} = \Delta S_\textrm{irreversible process} +\Delta S_\textrm{reversible process} = 0.$

The total entropy change is thus only reflected in the entropy change of the surroundings:

$\displaystyle \Delta S_\textrm{total} =\Delta S_\textrm{surroundings}.$

The surroundings can be considered a constant temperature heat reservoir and their entropy change is given by

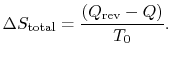
$\displaystyle \Delta S_\textrm{total} = \frac{(Q_\textrm{rev} - Q)}{T_0}.$

We also know that the total entropy change, for system plus surroundings is,

$\displaystyle \Delta S_\textrm{total} = \left[\Delta S_\textrm{irreversible pro... ...{\Delta S}_\textrm{reversible process}\right]_\textrm{system and surroundings}.$

The total entropy change is associated only with the irreversible process and is related to the work in the two processes by

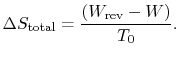
$\displaystyle \Delta S_\textrm{total} = \frac{(W_\textrm{rev} - W)}{T_0}.$

The quantity $W_\textrm{rev} -W$ represents the extra work required to restore the system to the original state. If the process were reversible, we would not have needed any extra work to do this. It represents a quantity of work that is now unavailable because of the irreversibility. The quantity $W_\textrm{rev}$ can also be interpreted as the work that the system would have done if the original process were reversible. From either of these perspectives we can identify $(W_\textrm{rev} -W)$ as the quantity we denoted previously as

, representing lost work. The lost work in any irreversible process can therefore be related to the total entropy change (system plus surroundings) and the temperature of the surroundings by

$\displaystyle \textrm{Lost work }= W_\textrm{rev} - W = T_0\Delta S_\textrm{total}.$

To summarize the results of the above arguments for processes where heat can be exchanged with the surroundings at :

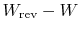$W_\textrm{rev} -W$ represents the difference between work we actually obtained and work that would be done during a reversible state change. It is the extra work that would be needed to restore the system to its initial state.
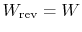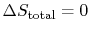For a reversible process, $W_\textrm{rev} = W$ ; $\Delta S_\textrm{total}=0$ .
For an irreversible process, 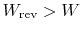W$"> ; 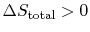0$"> .
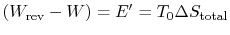$(W_\textrm{rev} -W)=E'=T_0\Delta S_\textrm{total}$ is the energy that becomes unavailable for work during an irreversible process.