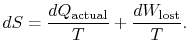6.5 Irreversibility, Entropy Changes, and ``Lost Work''
Consider a system in contact with a heat reservoir during a reversible process. If there is heat ![]() absorbed by the reservoir at temperature
absorbed by the reservoir at temperature ![]() , the change in entropy of the reservoir is
, the change in entropy of the reservoir is ![]() . In general, reversible processes are accompanied by heat exchanges that occur at different temperatures. To analyze these, we can visualize a sequence of heat reservoirs at different temperatures so that during any infinitesimal portion of the cycle there will not be any heat transferred over a finite temperature difference.
. In general, reversible processes are accompanied by heat exchanges that occur at different temperatures. To analyze these, we can visualize a sequence of heat reservoirs at different temperatures so that during any infinitesimal portion of the cycle there will not be any heat transferred over a finite temperature difference.
During any infinitesimal portion, heat ![]() will be transferred between the system and one of the reservoirs which is at
will be transferred between the system and one of the reservoirs which is at ![]() . If
. If ![]() is absorbed by the system, the entropy change of the system is
is absorbed by the system, the entropy change of the system is
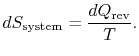
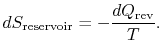
The conclusion is that for a reversible process, no change occurs in the total entropy produced, i.e., the entropy of the system plus the entropy of the surroundings: ![]() .
.
We now carry out the same type of analysis for an irreversible process, which takes the system between the same specified states as in the reversible process. This is shown schematically in Figure 6.7, with ![]() and
and ![]() denoting the irreversible and reversible processes. In the irreversible process, the system receives heat
denoting the irreversible and reversible processes. In the irreversible process, the system receives heat ![]() and does work
and does work ![]() . The change in internal energy for the irreversible process is
. The change in internal energy for the irreversible process is
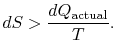 \frac{dQ_\textrm{actual}}{T}.$">
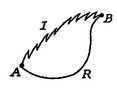
\frac{dQ_\textrm{actual}}{T}.$">The change in entropy for any process that leads to a transformation between an initial state ``a'' and a final state ``b'' is therefore
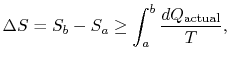
The difference ![]() represents work we could have obtained, but did not. It is referred to as lost work and denoted by
represents work we could have obtained, but did not. It is referred to as lost work and denoted by ![]() . In terms of this quantity we can write,
. In terms of this quantity we can write,
The content of Equation (6.4) is that the entropy of a system can be altered in two ways: (i) through heat exchange and (ii) through irreversibilities. The lost work ( ![]() in Equation (6.4)) is always greater than zero, so the only way to decrease the entropy of a system is through heat transfer.
in Equation (6.4)) is always greater than zero, so the only way to decrease the entropy of a system is through heat transfer.
To apply the second law we consider the total entropy change (system plus surroundings). If the surroundings are a reservoir at temperature ![]() , with which the system exchanges heat,
, with which the system exchanges heat,

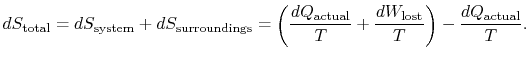
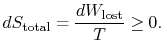
Yet another way to state the distinction we are making is
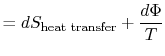 | ||
or | ||
Equation (6.5) can also be written as a rate equation,
The term
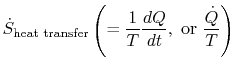
Muddy Points
Do we ever see an absolute variable for entropy? So far, we have worked with deltas only (MP 6.8)
I am confused as to ![]() as opposed to
as opposed to ![]() .(MP 6.9)
.(MP 6.9)
For irreversible processes, how can we calculate ![]() if not equal to
if not equal to ![]() ?(MP 6.10)
?(MP 6.10)
Disusun Ulang Oleh:
Arip Nurahman
Pendidikan Fisika, FPMIPA. Universitas Pendidikan Indonesia
&
Follower Open Course Ware at MIT-Harvard University. Cambridge. USA.
Materi kuliah termodinamika ini disusun dari hasil perkuliahan di departemen fisika FPMIPA Universitas Pendidikan Indonesia dengan Dosen:
1. Bpk. Drs. Saeful Karim, M.Si.
2. Bpk. Insan Arif Hidayat, S.Pd., M.Si.
Dan dengan sumber bahan bacaan lebih lanjut dari :
Massachusetts Institute of Technology, Thermodynamics
Professor Z. S. Spakovszk, Ph.D.
Office: 31-265
Phone: 617-253-2196
Email: zolti@mit.edu
Aero-Astro Web: http://mit.edu/aeroastro/people/spakovszky
Gas Turbine Laboratory: home
Kepada Para Dosen di MIT dan Dosen Fisika FPMIPA Universitas Pendidikan Indonesia
Semoga Bermanfaat
![$\displaystyle dS = \frac{dQ_\textrm{actual}}{T} +\frac{1}{T}\biggl[dW_\textrm{rev} -dW_\textrm{actual}\biggr].$](http://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/img711.png)